PROGRAMACIÓN LINEAL
2º Bachillerato Ciencias Sociales
 
3.- Programación Lineal con dos variables. Enunciado general.

En un problema de Programación Lineal con dos variables, x, y, se trata de optimizar (maximizar o minimizar) una función ( llamada función objetivo) de la forma

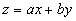Sujeta a una serie de restricciones dadas mediante un sistema de desigualdades lineales:

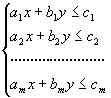
El conjunto de puntos que cumplen todas las desigualdades determinan un recinto, acotado o no, que se denomina conjunto de soluciones factibles.

La solución factible que hace óptima (máxima o mínima, según se desee) la función objetivo, se llama solución óptima.
4.- Posibles soluciones de un problema de Programación Lineal. 

Un problema de Programación Lineal con dos variables puede tener una solución, infinitas o ninguna, como se puede comprender observando los ejemplos gráficos siguientes. 

Supongamos que se pretende maximizar la función z: 

En el gráfico 1 la solución es única se alcanza el máximo en el punto B 

En el gráfico 2 hay infinitas soluciones porque el máximo se alcanza en todos los puntos entre A y B 

En el gráfico 3 no existe solución pues la función no alcanza nunca el máximo debido a que el recinto no está acotado superiormente. 

5.- Ejemplos
La siguiente escena corresponde a un problema de Programación Lineal con dos restricciones (más otras dos fijas x>=0 ; y>=0 que aparecen en casi todos los problemas). Aparecen los siguientes controles:

Función Objetivo: z=F1x+F2y que hay que hacer Max. (FMax=1) ó Min. (FMax=0)

Restricciones: con dos controles numericos >1, >2 para indicar el tipo de desigualdad (0=<, 1=>)
A1x+B1y<=C1
A2x+B2y<=C2
x>=0 ; y>=0

y dos cotroles gráficos el punto P(x,y) y el punto Q(x,y)

  
1.-Mueve el punto P(x,y) por cada uno de los recintos del 1º cuadrante (x>=0 ; y>=0) para saber el valor que van tomando A1x+B1y <?C1
A2x+B2y <?C2.

2.-Deja el punto P(x,y) en el recinto en que se verifiquen todas las desigualdades, aparecerá coloreado en turquesa el conjunto de Soluciones Factibles.
Represéntalo en tu cuaderno

3.- Con el punto Q(x,y) seleciona puntos del conjunto de  soluciones factibles y observa el valor que va tomando la función objetivo.

4.- Repite la operación pero probando con puntos de los bordes y vértices del recinto. (Puedes introducir directamente las coordenadas de Q.x y Q.y pulsando con el boton derecho sobre la escena)
5.- ¿En que punto se alcanza el valor máximo?. Para ayudarte a ver los vértices y la función objetivo pon el control S=1

6.- Anótalo todo en tu cuaderno

  

7.- Modifica  las desigualdades con los controles >1, >2, FMax y resuelve los siguientes problemas:
z=F1x+F2y  Min
A1x+B1y>=C1
A2x+B2y<=C2
x>=0 ; y>=0		 z=F1x+F2y  Min
A1x+B1y<=C1
A2x+B2y>=C2
x>=0 ; y>=0		 z=F1x+F2y Max
A1x+B1y>=C1
A2x+B2y>=C2
x>=0 ; y>=0

8.- Modifica las desigualdades y resuelve los siguientes problemas:

z=x+3y  Min
x+y<=5
x-y<=2
x>=0 ; y>=0		 z=x+y  Min
2x+y>=6
x+3y>=6
x>=0 ; y>=0		 z=2x-4y  Max
x-4y<=0
x+y<=10
x>=0 ; y>=0

 Si es necesario para ver mejor la escena modifica los controles de Zoom, O.x y O.y.

  
  ÍNDICE   INECUACIONES      
           
  Pedro J. Martín Romero
 
Ministerio de Educación, Cultura y Deporte. Año 2003