
 |
PROBLEMAS AFÍNS |
| Xeometría | |
| 5. Perpendicular dende un punto a un plano | |
A recta
r que
pasa por un punto P e é perpendicular a un plano π obtense
utilizando como
vector director da recta, 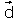 , o vector
normal do plano, , o vector
normal do plano, 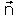 . .Calculando o punto de corte da recta e do plano pódese calcular a distancia entre o punto P e o plano π, e tamén o simetrico do punto P respecto do plano. |
|
Exemplo resolto Recta que pasa por P(1,0,1) e corta perpendicualrmente ao plano 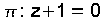 . .» O vector director da recta é o vector normal do plano: 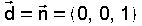 As ecuacións parámetricas da recta perpendicular: 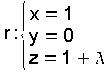 » Para calcular o punto de corte M, substitúese un punto xenerico da recta 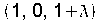 na ecuación do plano na ecuación do plano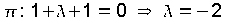 . . Daquela 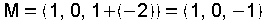 |
|
| 6. Perpendicular dende un punto a unha recta | |
| A recta
s que
pasa por un punto P
e é perpendicular a unha recta r
pode obterse por varios métodos. Un deles consiste en obter o plano α que é perpendicular a r e contén a P, e o plano β que contén a r e a P. A intersección destes dous planos será a recta buscada. Na escena pode verse a construcción do exemplo resolto |
|
| Exemplo resolto. Recta que pasa por P(3,-2,1) e corta perpendicualrmente á recta 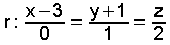 » O plano α que é perpendicular á recta r ten como vector normal 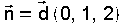 .polo que a súa ecuación é .polo que a súa ecuación é 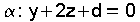 . .Como pasa por P, substituindo as súas coordenadas na ecuación do plano -2+2+d=0 queda d=0 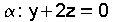 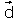 , o outro é o vector que une o punto
A(3,-1,0)
da recta e P
(2,-1,1). O vector normal será o produto vectorial destes dous , o outro é o vector que une o punto
A(3,-1,0)
da recta e P
(2,-1,1). O vector normal será o produto vectorial destes dous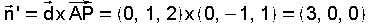 A ecuación do plano será 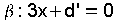 e
substituindo de novo o punto P: e
substituindo de novo o punto P: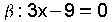 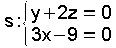 e o seu vector director
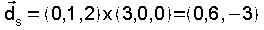 |
|
| 7. Perpendicular común a dúas rectas | |
| Un dos
métodos para obter unha recta perpendicular a dúas rectas, r e s, que se
cruzan basease na cosntrucción dos dous planos seguintes: Obtense o plano α que contén á recta r e é paralelo ao vector . Obtense o plano β que contén á recta s e é paralelo ao vector . A perpendicular común é a recta determinada por estes dous planos. |
|
| Exemplo resolto. Obter a perpendicular común as rectas 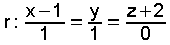 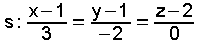 » O plano α ten como vectore directores 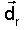 e e
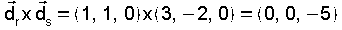 ,
que normalizado queda ,
que normalizado queda 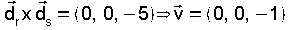 . .Entón o seu vector normal é 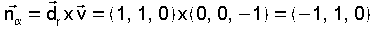 Ecuación 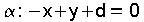 .
Substituindo o punto A(1,0,-2)
da recta r: -1+d=0,
entón d=1. .
Substituindo o punto A(1,0,-2)
da recta r: -1+d=0,
entón d=1.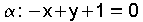 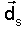 e e
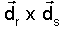 polo
que o seu vector normal será polo
que o seu vector normal será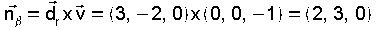 Ecuación 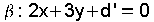 .
Substituindo o punto B(1,1,2)
da recta s:
2+3+d=0,
entón d=-5. .
Substituindo o punto B(1,1,2)
da recta s:
2+3+d=0,
entón d=-5.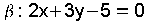 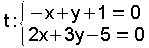 e o seu vector director
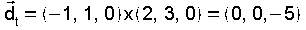 |
|
 |
 |
|||||
| Andrés Piñón Fernández | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2009 | ||

Os
contidos desta unidade didáctica están baixo unha licenza
de Creative Commons se non se indica o contrario.