
I.- Introducción
Existen ecuaciones que carecen de solución en el conjunto de los números reales. Por ejemplo, la ecuación x²+9=0 no tiene solución real ya que no existe ningún número real que elevado al cuadrado dé -9.
El matemático hindú Bhaskara (1114-1178) ya hacía referencia en su libro Lilavati a la inexistencia de la raíz cuadrada de un número negativo.
Gerolamo Cardano (1501-1576), matemático y médico italiano, fue el primero en escribir las raíces de números negativos solución de una ecuación de segundo grado, aunque especificando que no tenían sentido.
Euler (1707-1783) introdujo una nomenclatura específica para resolver raíces de números negativos.
Carl Friedrich Gauss (1777-1855) culminó la construcción de un nuevo conjunto numérico, el de los números complejos.
La unidad imaginaria, i, es el número que elevado al cuadrado da -1.
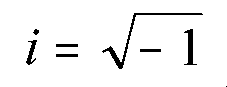
Una expresión de la forma a + b i, en la que a y b son dos números reales cualesquiera e i es la unidad imaginaria, se denomina número complejo.
Escribiremos z = a + b i, a es la parte real del número complejo z y b es la parte imaginaria de z. La expresión a + bi recibe el nombre de forma binómica del número complejo z.
Si la parte imaginaria es cero, tenemos un número real. Si la parte real es cero, un número imaginario puro.
II.- Representación gráfica de los números complejos.
Los números complejos se representan en un plano infinito que llamaremos plano complejo, de modo que la parte real se represente en el eje de abscisas, llamado EJE REAL, y la parte imaginaria en el eje de ordenadas, llamado EJE IMAGINARIO.
Actividades:
a).- Representa los siguientes números complejos: -3i, 2-3i, -3+i, 4, -5, 4i, 3+4i.
b).- Observa dónde aparecen representados los números reales y los números imaginarios puros.
c).- Mueve con el ratón el punto P y observa el signo de la parte real y la parte imaginaria según el cuadrante en que lo situemos.
III.- Suma, multiplicación y división de números complejos en forma binómica.
Sean los números complejos z = a + bi y w = c + di. Definimos:
Suma.- Para sumar dos o más números complejos se suman las partes real e imaginaria de cada uno de ellos.
Multiplicación.- Para multiplicar números complejos se aplica la propiedad distributiva teniendo en cuenta que i 2 = -1.
División.- Para dividir dos números complejos se multiplica el numerador y el denominador por el conjugado del denominador. (El conjugado de un número complejo es otro número complejo que tiene la misma parte real y la parte imaginaria cambiada de signo).

Actividades:
a).- Da a z los valores 2-5i, 1+5.5i, 6+3i, 1+3i, 3.5+2i y a w los valores -1+i, 0.5+0.5i, -1-1.5i, -2+0.5i, 0.5+2i. Calcula z+w, z.w y z/w. (Comprueba tus resultados con los de la escena).
IV.- Forma polar o módulo-argumental de un número complejo.
A cada número complejo z = a + bi se le asigna, en el plano complejo, un punto P de coordenadas (a,b).
Si se une el origen de coordenadas O con P, se obtiene el vector OP. De esta forma a todo número complejo se le asocia un vector fijo de origen O y extremo P (afijo del número complejo).
El punto P se puede determinar mediante sus coordenadas (a,b) o mediante la longitud del vector OP y el ángulo que éste forma con el eje positivo de abscisas.
Se llama módulo del número complejo z = a + bi, y se representa por m o |z|, a la longitud del vector OP.
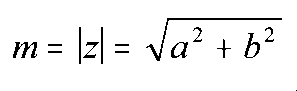
Se denomina argumento del número complejo z = a + bi, y se representa por a al ángulo que forma el vector OP con el semieje positivo de abscisas. Para determinar el valor de a se aplica la fómula:
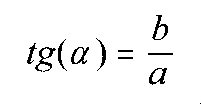
La determinación del argumento no es única ya que existen infinitos ángulos con la misma tangente. Si se restringe la determinación a ángulos comprendidos entre 0 y 2p (0° y 360°), existen dos ángulos, que difieren en p radianes (180°), con la misma tangente. El argumento dependerá de los signos de a y b, es decir, del cuadrante en el que está situado el afijo de dicho número complejo.
Notemos que a = m cos(a) y b = m sen(a). Escribiremos z = a+bi = za = m(cos a +i sen a ).
Actividades:
a).- Observa el valor de la parte real y de la parte imaginaria del número complejo z cuando el argumento sea 0°, 90°, 180° y 270°.
b).- Observa el valor de la parte real y de la parte imaginaria del número complejo z cuando el argumento sea 45°, 135°, 225° y 315°.
c).- Puedes mover con el ratón el punto P y observar el argumento dependiendo del cuadrante en que se encuentre el punto P.
d).- Observa qué ocurre cuando la parte real es cero. (No existe la tangente de 90° ni la tangente de 270°).
V.- Raíces n-ésimas de la unidad.
Si calculamos las raíces n-ésimas de 1 y representamos sus correspondientes afijos obtenemos los vértices de un polígono regular con un número de lados igual al índice de la raíz.
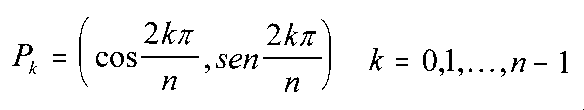
Los vértices del polígono estarán sobre la circunferencia de radio 1.
Actividades:
a).- Aumenta el índice de la raíz y observa lo que ocurre.
VI.- Operaciones con números complejos y transformaciones geométricas.
1.-Si se suma el número complejo a + bi a otro número complejo c + di, se produce una traslación de vector v=(a,b). Vamos a hacer translaciones del triángulo PQR. Obtendremos el triángulo P1Q1R1
Actividades:
a).- Haz coincidir los dos triángulos.
b).- Haz distintas traslaciones cambiando los valores de a y b. Puedes mover con el ratón el punto P.
2.-Si se multiplica el número complejo 1a a otro número complejo , se produce un giro de centro el origen y ángulo a
Vamos a girar el triángulo de vértices PQR.
Actividades:
a).- Haz distintos giros. Puedes mover con el ratón el punto P.
3.-Si multiplicamos por el número complejo za a otro número complejo , realizamos una homotecia de centro O y razón módulo de z y un giro de centro O y ángulo a
Vamos a multiplicar los afijos de los vértices del triángulo PQR por za
Actividades:
a).- Observa que si el módulo es mayor que 1, el triángulo transformado P1Q1R1 es mayor que el triángulo PQR.
b).- Observa que si el módulo es menor que 1, el triángulo transformado P1Q1R1 es más pequeño que el triángulo PQR. (Puedes mover con el ratón el punto P. Cambia la escala para ver bien la escena.).
Autor: Mariano Banzo Marraco.