y los de su raíz
n-ésima 
:
RAÍCES N-ÉSIMAS
Los números reales positivos tienen dos raíces cuadradas. Por ejemplo, 2 y -2 son las raíces de 4.
Los números reales negativos tienen dos raíces cuadradas imaginarias. Puedes comprobar, elevándolos al cuadrado que 2i y -2i son las raíces de -4.
Vamos a probar ahora que cualquier número complejo, salvo el 0 , tiene n raíces n-ésimas.
Obtención de las raíces n-ésimas de un número complejo
Estudiemos la relación que hay
entre el módulo y el argumento de y los de su raíz
n-ésima :
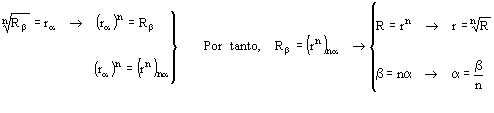
La raíz n-ésima de
un número complejo |
Utiliza la siguiente escena para hallar las raíces n-ésimas:
Selecciona el módulo r y el argumento A del número complejo que vamos a utilizar para hallar sus raíces.
Elige el índice de la raíz n.
Obtén las n raíces sucesivamente (en forma binómica y polar) dando a k los valores 0,1,2,...,n-1
Un número complejo, Sus argumentos son:
Para n > 2 los afijos de estas n raíces son los vértices de un n-ágono regular con centro en el origen. |
Utiliza la siguiente escena para representar gráficamente las raíces n-ésimas:
Selecciona el módulo r y el argumento A del número complejo que vamos a utilizar para hallar sus raíces.
Limpia la escena pulsando en el botón limpiar
Elige el índice de la raíz n.
Limpia la escena.
Obtén la representación gráfica de las n raíces sucesivamente dando a k los valores 1,2,...,n-1.(la raíz correspondiente a k=0 se representa automáticamente).
13.- Calcula las siguientes raíces y representa gráficamente sus soluciones (Indicación: Para obtener las raíces n-ésimas el número complejo tiene que estar expresado en forma polar):
Autor: Inmaculada Ascaso Martínez
y un argumento 
