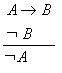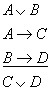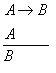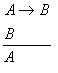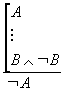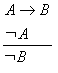LÓXICA
Aplicación da lóxica ós
ordenadores
Principais
regras derivadas
Falacias
formais (razonamentos incorrectos)
Nas regras con dobre raia a
operación pode realizarse en senso inverso. Cando apareza
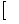indica que todo o que está
dentro do corchete non está demostrado e depende do suposto de que se
parte, non poderá ser usado fora do mesmo.
|
Aplicación
da lóxica ós ordenadores
INTRODUCCIÓN
Como
é sabido a linguaxe básica ca que traballan os ordenadores é a
denominada linguaxe de máquina, que funciona coma unha linguaxe formal,
binaria, é dicir, ven sendo un circuito eléctrico onde só hai dous valores:
un circuito aberto e un circuito pechado..
Considerando
un cicuito aberto como a falsedade lóxica (valor 0), un circuito pechado
como a verdade lóxica (valor 1), veráse a relación entre a linguaxe lóxica e
a dos ordenadores. O operador conxuntor require interruptores en liña, o
disxuntor require interruptores en paralelo.
Se
representamos un interruptor ou un conmutador que deixa pasar a electricidade
por unha porta en cor verde, un interruptor ou conmutador que impide
o paso da electricidade por unha porta en cor branco , unha saída
de electricidade , por exemplo, unha bombilla encendida coma un
círculo amarelo (equivalente a valor de verdade 1), e unha apagada igual pero
en cor gris (valor de verdade 0), podemos presentar gráficamente
distintas proposicións lóxicas.
OPERADOR NEGADOR
Este é un operador monádico que vai diante
de calquera fórmula ben formada, por exemplo p,
á que lle cambia o seu valor de verdade. Represéntase Ø
e lese "non"
-
Proba a modifica-los
valores de p
e
observa o resultado.
-
En base ós anteriores
resultados elabora a táboa de verdade para
non p
OPERADOR CONXUNTOR
É un operador binario que une dúas formulas
ben formadas, por exemplo p
e q
, escríbese Ù
entre dúas fófmulas ben formadas e lese "e"
Exemplo:
p
Ù q
-
Proba a modifica-los valores
de p
e
q e
observa o resultado.
-
En base ós anteriores
resultados elabora a táboa de verdade para
p
e q
-
Pon un exemplo en linguaxe
natural.
OPERADOR DISXUNTOR
É un operador binario que une dúas formulas
ben formadas, por exemplo p
e q
. Existen dous tipos de disxuntor, o exclusivo (w)
e o inclusivo que se presenta aquí. O disxuntor inclusivo escríbese Ú
entre dúas fórmulas ben formadas e lese "ou"
Exemplo: p
Ú q
-
Proba a modifica-los valores
de p
e
q
e
observa o resultado.
-
En base ós anteriores
resultados elabora a táboa de verdade para
p
ou q
-
Busca exemplos da linguaxe
natural que se correspondan ó disxuntor inclusivo asi como ó disxuntor
exclusivo. Observa que expresións se usan na linguaxe natural para ós
disxuntores.
OPERADOR BICONDICIONAL
Tamén serve para unir dúas fórmulas
ben formadas, de modo que é un operador binario, por exemplo
p
e q
, escríbese
«
entre dúas fórmulas ben formadas e lese "se
e só se"
Exemplo: p
«
q
-
Proba a
modifica-los valores de p e
q e observa o resultado.
-
En base ós anteriores
resultados elabora a táboa de verdade para
p
se e só se q
OPERADOR CONDICIONAL
Denomínase tamén implicador, é un operador
binario que une dúas fórmulas, por exemplo
p
e q
, escríbese
®
entre dúas fórmulas ben formadas e lese "se
... entón ..."
Exemplo:
p
®
q
(se p entón q)
-
Proba a modifica-los valores
de p
e
q
e
observa o resultado.
-
En base ós anteriores
resultados elabora a táboa de verdade para
se
p entón q
|
|
|
Fai as táboas de verdade das seguintes
fórmulas e indica de que tipo son :
Exercicio 1
(Ø p «
Ø q ) ® [( p Ú
Ø q ) Ù ( q Ú
Ø p )]
Exercicio 2
[ Ø ( p «
Ø q ) Ù p ] ®
( q Ú Ø q )
Exercicio 3
( p Ù Ø
q ) « ( Ø p Ú
q )
Exercicio 4
[ (p ® q ) Ú
( Ø q ®
Ø p ) ] «
Ø q
|
|
|
| Exercicio 5
Deduce a conclusión :
-- 1. (p ® q) Ù
(q ® Ø r)
--2. r Ù Ø
[Ø p Ù Ø
(t Ù s)]
Conclusión: s
|
| Exercicio 6
Deduce a conclusión :
-- 1. Ø (s Ù
q )
--2. Ø q ®
Ø t
--3. Ø s ®
p
Conclusión: Ø t Ù
Ø p
--4. Ø p
|
|
|
| Exercicio 7
Formaliza e analiza o argumento exposto e indica
se e correcto ou non e por que mediante o uso das regras de deducción :
"A profesora de filosofía díxome
que, se eu non facía tódolos traballos, non me aprobaría a asignatura.
Realice tódolos traballos, de modo que debería aprobármela. ¿Non é
así?"
|
| Exercicio 8
Pasa a linguaxe formal e deduce a conclusión (indica
que variable lle das a cada proposición) :
"A situación é moi complicada e
non existe solución. Evidentemente careces de sentido do humor e tes
sentido do humor ou acabas desesperándote. Do que se deduce que a
situación é moi complicada e estás desesperado"
|
| Exercicio 9
Pasa a linguaxe formal e deduce a conclusión
(indica
que variable lle das a cada proposición):
"Ou troca a situación política
mundial ou aumentará a inmigración. Non hai progreso na calidade de vida
dos paises do "sur". Se troca a situación política
mundial, os paises do "sur" terán mellor calidade de vida.
Se aumenta a inmigración, cómpre promover actitudes de tolerancia. De
modo que é necesario educar na tolerancia.
|
| Exercicio 10
Formaliza e analiza o argumento exposto . Sinala
cales son as conclusións correctas mediante o uso das regras de
deducción :
"O detective Pazos exercita as súas
capacidades deductivas, no caso que hoxe lle ocupa dispón destes datos:
--1 Ou o asasinato cometeuse de noite na
máis absoluta oscuridade ou o principal sospeitoso é cego.
--2 Ou o principal sospeitoso non é ceego
ou minte ó declarar que non viu nada.
--3 Ou non minte ou o detector de
mentiras "Pazo’s" está estropeado.
--4 O caso é que o citado detector é
infalible (non pode estar estropeado xamais)
¿Minte ou non minte o sospeitoso? ¿É
cego ou non o é? ¿Cometeuse o asasinato de día ou de noite? |
|
Exercicios: 1 / 2 /
3 / 4 / 5 / 6 / 7 / 8
/ 9 / 10 |
| Exercicio 1
(Ø p «
Ø q ) ®
[( p Ú Ø
q ) Ù ( q Ú Ø p )]
É unha tautoloxía ou lei lóxica
|
( Ø
p
|
«
|
Ø q )
|
®
|
[( p
|
Ú
|
Ø q )
|
Ù
|
( q
|
Ú
|
Ø p )]
|
|
0
1
|
1
|
0 1
|
1
|
1
|
1
|
0 1
|
1
|
1
|
1
|
0 1
|
|
1
0
|
0
|
0 1
|
1
|
0
|
0
|
0 1
|
0
|
1
|
1
|
1 0
|
|
0
1
|
0
|
1 0
|
1
|
1
|
1
|
1 0
|
0
|
0
|
0
|
0 1
|
|
1
0
|
1
|
1 0
|
1
|
0
|
1
|
1 0
|
1
|
0
|
1
|
1 0
|
Exercicio 2
[ Ø ( p «
Ø q ) Ù
p ] ® ( q Ú Ø q )
É unha tautoloxía ou lei lóxica
|
[ Ø
|
( p
|
«
|
Ø q )
|
Ù
|
p ]
|
®
|
( q
|
Ú
|
Ø q )
|
|
1
|
1
|
0
|
0
1
|
1
|
1
|
1
|
1
|
1
|
0
1
|
|
0
|
0
|
1
|
0
1
|
0
|
0
|
1
|
1
|
1
|
0
1
|
|
0
|
1
|
1
|
1
0
|
0
|
1
|
1
|
0
|
1
|
1
0
|
|
1
|
0
|
0
|
1
0
|
0
|
0
|
1
|
0
|
1
|
1
0
|
Exercicio 3
( p Ù Ø q )
« ( Ø p Ú q )
É unha inconsistencia ou contradicción lóxica
|
( p
|
Ù
|
Ø
q )
|
«
|
(Ø
p
|
Ú
|
q )
|
|
1
|
0
|
0
1
|
0
|
0
1
|
1
|
1
|
|
0
|
0
|
0
1
|
0
|
1
0
|
1
|
1
|
|
1
|
1
|
1
0
|
0
|
0
1
|
0
|
0
|
|
0
|
0
|
1
0
|
0
|
1
0
|
1
|
0
|
Exercicio 4
[ (p ® q ) Ú
( Ø q ®
Ø p ) ] «
Ø q
É unha consistencia lóxica
|
[ (p
|
®
|
q )
|
Ú
|
( Ø q
|
®
|
Ø p )
]
|
«
|
Ø q
|
|
1
|
1
|
1
|
1
|
0
1
|
1
|
0
1
|
0
|
0
1
|
|
0
|
1
|
1
|
1
|
0
1
|
1
|
1
0
|
0
|
0
1
|
|
1
|
0
|
0
|
0
|
1
0
|
0
|
0
1
|
0
|
1
0
|
|
0
|
1
|
0
|
1
|
1
0
|
1
|
1
0
|
1
|
1
0
|
Exercicio 5
|
| |
Mª
Ángeles Costa Giráldez |
 |
|
|
Ministerio de Educación, Cultura y Deporte. Año 2002 |
| |
|
