
 |
Límites de funciones: Límite en un punto (idea intuitiva) II. |
| Análisis. | |
| Introducción. | |
|
Además de los casos analizados en la página anterior, puede suceder que el comportamiento de la función sea diferente a ambos lados del punto a, en otras palabras, la función toma valores muy distintos a la izquierda o a la derecha del punto a.
A continuación vamos a describir con algunos ejemplos este concepto.
| |
| Caso 5. | |
|
Los valores de la función f(x) se aproximan a un cierto número real, b, cuando la variable independiente se aproxima al punto a por la izquierda y a otro número real, c, cuando la variable independiente se aproxima por la derecha. | |
|
Acerca la x al valor de a en la imagen siguiente y comprueba cómo cuando x se acerca al punto a por la izquierda (línea blanca), f(x) se aproxima a b (línea verde) y cuando x se acerca al punto a por la derecha (línea turquesa), f(x) se aproxima a c (línea naranja). | |
|
Expresaremos este hecho mediante las siguientes expresiones:
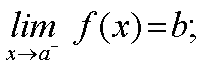 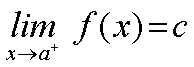
Y diremos que b es el límite de f(x) cuando x tiende al punto a por la izquierda y c es el límite de f(x) cuando x tiende al punto a por la derecha. | |
|
OBSERVACIÓN: Aunque los límites laterales existan, si éstos no coinciden diremos que no existe límite de la función en ese punto. Es decir, es necesario para que exista límite en un punto que los límites laterales existan y coincidan. | |
| Caso 6. | |
|
Los valores de la función f(x) aumentan indefinidamente cuando la variable independiente se aproxima al punto a por la derecha y se aproximan a un valor concreto (b) cuando la x se aproxima al punto a por la izquierda. | |
|
Acerca la x al valor de a en la imagen siguiente y comprueba cómo cuando x se acerca al punto a (línea blanca) por la derecha, f(x) se hace tan grande como se quiera (línea verde). Desplaza hacia arriba la gráfica y cambia la escala si es preciso para visualizarlo mejor. Y cuando x se acerca al punto a por la izquierda (línea turquesa), f(x) se acerca a b (línea naranja). | |
|
Expresaremos este hecho mediante las siguientes expresiones:
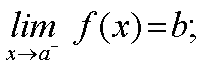 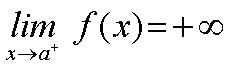
Y diremos que el límite de f(x) cuando x tiende al punto a por la derecha es infinito y el límite por la izquierda es b. | |
| Caso 7. | |
|
Los valores de la función f(x) disminuyen indefinidamente cuando la variable independiente se aproxima al punto a por la izquierda y crecen por la derecha. | |
|
Acerca la x al valor de a en la imagen siguiente y comprueba cómo cuando x se acerca al punto a (línea blanca), f(x) se hace tan pequeña (o tan grande) como se quiera (línea verde). Desplaza hacia abajo (o hacia arriba) la gráfica y cambia la escala si es preciso para visualizarlo mejor.
| |
|
Expresaremos este hecho mediante las siguientes expresiones:
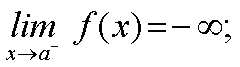 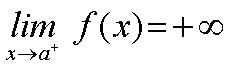
Y diremos que el límite de f(x) cuando x tiende al punto a por la izquierda es menos infinito y el límite por la derecha es más infinito. | |
| José Luis Alonso Borrego | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||
![]()
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.