8. La derivada de algunas funciones especiales

Hasta este momento se han manejado solamente  funciones derivables de todo orden; es decir, funciones cuya derivada es a su vez derivable, esta última también lo es, y así sucesivamente. 

El propósito de esta sección es explorar las derivadas de funciones que no se ajustan al patrón antes mencionado; es decir, funciones continuas no derivables en uno o varios puntos o funciones derivables cuya derivada  es no derivable en algún punto.

Puede apreciarse la potencia del Trazador de Derivadas en el hecho de que permite visualizar la función derivada de prácticamente cualquier función de las estudiadas en los cursos de cálculo, gracias a lo extenso de la biblioteca de DESCARTES.

Cabe advertir que en cada ejemplo, es necesario que el alumno complete el trazo de la función derivada, manteniendo oprimida la flecha ascendente del control "x".

8.1 Ejemplo 1. 


En la siguiente escena se muestra la gráfica de la función, 

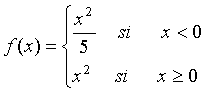
cuya derivada existe en cada punto de su dominio. 

  • Verifique que esta función  es derivable en cada punto. Asigne a  x cualquier valor  y alterne valores positivos y negativos de h. Observará que la recta secante para h = 0.0001 es aproximadamente igual a la recta secante para h = -0.0001, es decir son rectas muy parecidas a la recta tangente.

Ejemplo 2

 

 

 

 

 

 

 

 

 

 

 

 

 

8.2 Ejemplo 2. 


En la siguiente escena se muestra la gráfica de la función

 

cuya función derivada no está definida en x = 0, tal como lo muestra el Trazador de Derivadas; es decir, se trata de una función no derivable en un punto de su dominio.

 

  • Verifique que esta función no es derivable en x = 0, alternando valores positivos y negativos de h . Observará que en x=0, la recta secante para h = 0.0001 es aproximadamente igual a la recta y = x,  y para h = -0.0001 a la recta y = -x; es decir, no existe una recta a la cual se aproximan estas rectas secantes. 

  • Nótese que para cualquier valor de x diferente de cero, las rectas secantes si se aproximan a una recta (tangente) independientemente del signo de h pequeña.

 

 Ejemplo 3

 

 

 

 

 

 

 

 

 

 

 

 

8.3 Ejemplo 3. 


En la siguiente escena se muestra la gráfica de la función:

cuya función derivada no está definida en x = -1  y en x = 1, tal como lo muestra el Trazador de Derivadas; es decir, se trata de una función no derivable en dos puntos de su dominio. 

 

  • Verifique que esta función no es derivable en 
    x     = -1 y en x = 1, alternando valores positivos y negativos de h . Por ejemplo asigne a x el valor 1 y vea como es la recta tangente para h = 0.0001, a continuación cambie h a -0.0001 y observará que la recta secante cambia abruptamente, es decir no existe una recta a la cual se aproximen estas secantes, lo cual significa que no existe la recta tangente en este valor de x o bien también decimos que la función no es derivable en este punto.

  • Nótese que para cualquier valor de x diferente de cero, las rectas secantes si se aproximan a una recta (tangente) independientemente del signo de h pequeña.

 

La derivada de la función seno

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.