Extracte
de la pàgina http://www.xtec.es/~bfiguera/curioso.html#quadrat
Autor: Blai Figueras Álvarez
NOMBRES AL QUADRAT
Distància entre nombres
al quadrat
"La
distància o diferència entre 2 nombres consecutius al quadrat és la suma dels dos".
Exemples:
8² = 64 i 9² = 81. La seva diferència 81 - 64 = 17, és
a dir, 9 + 8 = 17
Això serveix en tots els casos... 24² = 576,
25² = 625, la diferència és 49 = 24 + 25
A partir d'aquí podem definir que la distància entre 2 nombres
qualssevol al quadrat és la coneguda fórmula, tantes vegades memoritzada,
però potser no sempre valorada en aquest aspecte del càlcul: "La
distància entre 2 nombres qualssevol al quadrat és la suma per la diferència".
a² - b²
= (a + b) · (a - b)
Exemple:
9² = 81, 5² = 25, 81 - 25 = 56, és a dir: (9 + 5) · (
9 - 5 ) = 14 x 4 = 56
Això, òbviament, ens pot permetre
calcular nombres al quadrat a partir dels que ja coneixem:
Ex. Quant serà 26²,
si sabem que 25² = 625 ?
Només hem de sumar 25 +
26 = 51, i afegir això al 625, o sigui, 625 + 51 = 676
Exercici: Quant és 37²,
si sabem que 30² = 900 ? >>>
Suma = 67, Diferència = 7
Amb una mica d'habilitat calcularem
67 x 7 = 469 i el sumarem a 900, per obtenir: 37² = 1.369
EXERCICI: Quant
és 54², si sabem que 50² = 2.500 ?
Quina serà la diferència entre 41² i 26²
?
- Un
mètode ràpid de calcular nombres al quadrat
-
-
a) Començaré amb el quadrat
dels nombres de 2 xifres acabats en 5:
El
quadrat dels nombres
tipus 15, 25, 35, etc. es poden fer de forma molt ràpida: "Multiplicant
la desena pròpia per la següent i afegint un 25 darrere"
-
Anem a veure alguns exemples:
Ex. 15²: multipliquem la seva desena 1
per la següent 2, i obtenim 2
afegim un 25 darrere i tenim el 225, que és 15².
Ex. 45² : 4
x 5 = 20, afegim el 25 i surt 2.025 = 45²
Ex. 65² : 6
x 7 = 42, afegim el 25 i ja tenim el 65² = 4.225
(sorprenent o no?)
-
-
b) Quadrat dels nombres de
dues xifres acabats en 1:
El
quadrat dels nombres
tipus 11, 21, 31, etc. es pot calcular de manera ràpida en tres parts: "Quadrat
de la desena, el doble de la desena, afegim un 1"
-
Exemples: 11²: quadrat de la desena 1 x 1 = 1
el doble de la desena 1 + 1 = 2
li afegim un 1 >>>> i obtenim el 121 = 11²
Ex. 31²: quadrat
de la desena 9, el doble de la desena 6, li afegim un 1
>>> 31² = 961 Si la suma
de les desenes passa de 9, aleshores en portem 1 quan construïm el nombre:
-
Ex. 61²: quadrat de la desena 36, el doble de la
desena 12 en aquest cas, com que passa de 9 la suma
en portem 1, o sigui, 372, i li afegim un 1 >> 61²
= 3.721
-
-
c) Quadrat dels nombres de
dues xifres acabats en 9:
El quadrat dels nombres tipus 19, 29, 39, etc. es poden calcular de manera ràpida en tres parts: "Al quadrat de la desena següent li afegim el 0, restem el doble de la desena següent i afegim
un 1"
-
Ex. 29²: quadrat de la
desena següent 3 x 3 = 9, afegim el 0, o sigui, 90
li restem el doble de la desena 3 + 3 = 6, és a dir, 90 - 6 = 84
li afegim un 1 >>>> i obtenim el 841 = 29²
Ex. 49²:
quadrat de la desena següent 25 >> 250, restem el doble de la desena
següent 10, 250 - 10 = 240, li afegim un 1 >>> 49² = 2401
-
-
d) Quadrat dels nombres de dues xifres acabats en 2 (i les altres xifres del 3 al 8):
D'una manera semblant als acabats en 1, farem els acabats en 2: "Quadrat de
la desena, el doble de la desena per 2, afegim un 4 (quadrat
del 2)"
-
Ex:
22²: quadrat de la desena 2
x 2 = 4
el doble de la desena 2 + 2 = 4 per 2 >> 8
li afegim un 4 >>>> i obtenim el 484 = 22²
Ex: 52²:
quadrat de la desena 5 x 5 = 25
el doble de la desena 10 per 2 = 20, és a dir, en portem 2, per
tant, 25+2 = 27 >> 270
li afegim un 4 >>>> i obtenim el 2704 = 52²
-
El mètode es pot generalitzar
per als altres nombres.
-
Per acabar anem a veure els nombres acabats en 3: "Quadrat de la desena, el doble
de la desena per 3, afegim un 9 (quadrat del 3)"
-
Ex. 73²: quadrat de la desena 7 x
7 = 49
el doble de la desena 7 + 7 = 14 per 3 >> 42, en portem 4, per
tant, 49+4 = 53 >> 532
li afegim un 9 >>>> i obtenim el 5.329 = 73²
EXERCICI: Calcular amb aquest mètode els següents nombres
al quadrat:
35² = ... ; 41² = ... ;
32² = ... ; 75² = ... ;
59² = ... ; 115² = ...
Mètode
dels "productes equidistants"
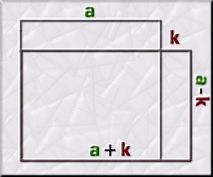 Un aspecte interessant dels
nombres
al quadrat és la "pèrdua" que es produeix si augmentem i disminuïm els nombres en una quantitat constant, és a dir, la diferència d'àrea entre
quadrats i rectangles amb un mateix perímetre.
Un aspecte interessant dels
nombres
al quadrat és la "pèrdua" que es produeix si augmentem i disminuïm els nombres en una quantitat constant, és a dir, la diferència d'àrea entre
quadrats i rectangles amb un mateix perímetre.
Prenem un quadrat de costat a i el convertim en un rectangle de costats: a
+
k ia
-
k.
Anem a veure què passa amb un exemple numèric: 24²
= 576
>
25 x 23 = 575 (-1)
Hem sumat i restat 1 i la distància és 1²
>
26 x 22 = 572 (-4)
Hem sumat i restat 2 i la distància és 2²
>
27 x 21 = 567 (-9)
Hem sumat i restat 3 i la distància és 3²
>
28 x 20 = 560 (-16)
Hem sumat i restat 4 i la distància és 4²
> 29 x 19 = 551 (-25)
Hem sumat i restat 5 i la distància és 5²
Podem concloure, doncs, que:
"La diferència
entre l'àrea d'un quadrat i l'àrea d'un rectangle,
generat a partir d'aquell, és igual al quadrat de la deformitat aplicada"
D'aquí també se'n pot treure una aplicació numèrica en el càlcul ràpid
del producte de nombres que siguin equidistants a un nombre
al quadrat, així, si observem que 18 i 12 són equidistants al
15, podrem calcular molt ràpidament 18 x 12, ja que 15²
= 225 i la distància
és 3² = 9,
deduïm que 18 x 12 = 216.
Només es pot aplicar quan els dos factors són parells o els dos senars.
Aquest "mètode dels productes equidistants" és molt eficaç amb l'única condició de memoritzar una bona sèrie de nombres al
quadrat i d'observar ràpidament si un producte ho permet o no.
EXERCICI: Calcular amb aquest mètode aquells productes que permetin
la seva aplicació:
29 x 21 = ... ; 35 x 30 = ... ; 18 x 12 = ... ; 23 x 31 = ... ; 37 x 32
= ... ; 54 x 46 = ...
TRIANGLES PITAGÒRICS
ENTERS
Expressions matemàtiques
per obtenir triangles rectangles amb valors enters
-
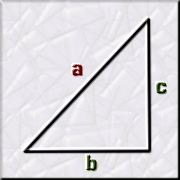 El gran Pitàgores de Samos ens va llegà el seu arxiconegut Teorema
dels triangles rectangles, pilar fonamental de càlculs
geomètrics i trigonomètrics, en què es relacionen les
mesures dels catets i de la hipotenusa: a²
= b² + c²
El gran Pitàgores de Samos ens va llegà el seu arxiconegut Teorema
dels triangles rectangles, pilar fonamental de càlculs
geomètrics i trigonomètrics, en què es relacionen les
mesures dels catets i de la hipotenusa: a²
= b² + c²
-
Com que quan apliquem aquesta fórmula matemàtica hem d'acabar
calculant una arrel quadrada, quasi sempre ens trobarem que
no obtenim valors exactes, o més ben dit, valors enters.
Al mateix Pitàgores li devem el triangle rectangle
arquetipus de mides 3, 4 i 5, però si pretenem utilitzar altres triangles rectangles amb valors enters
quasi mai ho aconseguirem i acabarem recorrent a aquest triangle
pitagòric (3, 4, 5) o als seus múltiples.
Dedico aquesta secció a exposar unes expressions matemàtiques
que
ens permetran obtenir la majoria dels triangles
rectangles de valors enters que existeixen, són fruït d'una bona idea inicial i d'un estudi exhaustiu posterior. Així que podeu prendre nota i, d'aquesta manera, tenir una petita eina amb la que podreu generar problemes, etc. que sempre tinguin com a solució valors enters, o simplement veure aquest capítol
com una curiositat matemàtica més.
-
La primera expressió ens genera les 3 mides de triangles
rectangles en què el catet petit és un nombre senar:
2n
+ 1, 2n(n + 1),
2n²
+ 2n + 1
-
Així per n = 1 obtenim els valors: 3,
4 i 5
(us
sona?). Per n = 2: 5,
12,
13,
etc.
-
La segona expressió ens genera les 3 mides de triangles
rectangles en què el catet petit és un nombre
parell:
2(n
+ 1), n(n + 2),
n²
+ 2n + 2
-
Ex. per n = 1 obtenim els valors: 4,
3
i 5 (altra vegada). Per n = 3: 8,
15,
17,
etc.
Anem a veure una taula amb els 7 primers valors de cadascuna:
-
-
|
2n + 1
|
2n(n + 1) |
2n²
+ 2n + 1 |
n
|
2(n
+ 1) |
n(n
+ 2) |
n²
+ 2n + 2 |
|
3 |
4 |
5 |
1 |
4 |
3 |
5 |
|
5 |
12 |
13 |
2 |
6 |
8 |
10 |
|
7 |
24 |
25 |
3 |
8 |
15 |
17 |
|
9 |
40 |
41 |
4 |
10 |
24 |
26 |
|
11 |
60 |
61 |
5 |
12 |
35 |
37 |
|
13 |
84 |
85 |
6 |
14 |
48 |
50 |
|
15 |
112 |
113 |
7 |
16 |
63 |
65 |
-
A les dues expressions exposades
hi hauríem d'afegir una constant k, que en multiplicar-la
per cadascun dels valors obtinguts i prenent diferents valors ens permeti obtenir els múltiples d'aquestes mides, que òbviament,
també satisfan el Teorema de Pitàgores:
-
[2n
+ 1, 2n(n + 1), 2n²
+ 2n + 1] · k
[2(n
+ 1), n(n + 2), n²
+ 2n + 2] · k
-
Ara ja teniu un bon grapat d'exemples i amb les expressions matemàtiques podreu obtenir-ne més.
De totes maneres aquests no són els únics
i, per això, vaig acabar buscant un altre algoritme de càlcul més general.
Partint de la coneguda regla, exposada
en el capítol anterior, que diu que:
-
"La distància entre 2 nombres qualssevol al quadrat és la
suma per la diferència"
x² - y²
= (x + y) · (x - y)
-
Es pot fer la següent demostració:
Si tenim un nombre a, que és múltiple d'altres,
el podrem expressar com a = x · y
Segons
el Teorema de Pitàgores: a²=
c²-
b²
= (c + b) · (c - b)
D'aquí podem deduir que: x² · y² =
(c + b) · (c - b), i per tant:
x²
= c + b
y² = c - b Si
ara resolem aquest sistema d'equacions tindrem:
-
c
=
(x²
+ y²) / 2 , b =
(x² - y²) / 2
, a = x · y
-
O sigui, donat un catet que amida a el podrem expressar en forma de producte de dos divisors: x · y (fins i tot els nombres primers: a = a · 1 => x = a, y = 1, satisfan
aquesta fórmula => veure la taula) i a partir d'aquests trobem que: l'altre
catet és la meitat de la diferència dels quadrats dels seus divisors i la seva hipotenusa
és la meitat de la suma dels quadrats dels seus divisors.
-
L'únic petit problema que sorgeix aquí és que com que hem de dividir per 2 en alguns casos (si un divisor és parell i l'altre senar) no surten valors exactes, però els seus múltiples parells sí que ho seran i, en qualsevol cas, com a màxim
tindrem un decimal .5 també molt interessant.
Anem a veure ara uns quants exemples:
-
-
|
a = x · y |
b=
(x² - y²) / 2 |
c=
(x² + y²) / 2 |
a = x · y |
b=
(x² - y²) / 2 |
c=
(x² + y²) / 2 |
|
27 = 9 · 3 |
(9² - 3²) / 2 =
36 |
(9² + 3²) / 2 =
45 |
45 = 15 · 3 |
(15² - 3²) / 2 =108 |
(15² + 3²) / 2 =117 |
|
32 = 8 · 4 |
(8² - 4²) / 2 =
24 |
(8² + 4²) / 2 =
40 |
48 = 8 · 6 |
(8² - 6²) / 2 =
14 |
(8² + 6²) / 2 =
50 |
|
33 = 11 · 3 |
(11² - 3²) / 2 =
56 |
(11² + 3²) / 2 =
65 |
17 = 17 · 1 |
(17² - 1²) / 2 =144 |
(17² + 1²) / 2 =145 |
|
35 = 7 · 5 |
(7² - 5²) / 2 =
12 |
(7² + 5²) / 2 =
37 |
36 = 9 · 4 |
(9² - 4²) / 2 = 32.5 |
(9² + 4²) / 2 = 48.5 |
En aquest últim exemple tenim a =
36, b =
32.5, c =
48.5, d'aquí podem deduir que els seus múltiples
parells sí són enters com: a =
72, b =
65, c =
97, a =
144, b =
130, c =
194, etc.
-
Fins aquí aquest estudi, per
concloure només diré que encara queda un grup de triangles
rectangles de valors enters que no es generen amb cap de les expressions exposades, però sí que amb aquestes obtindrem la
majoria dels que existeixen i, per tant, em semblen de gran utilitat.
- Càlcul
de la diagonal d'una figura geomètrica que no existeix!
-
- Si volem calcular la mesura la
diagonal d'un quadrat coneixent la mida dels seus costats, només necessitarem aplicar el Teorema de Pitàgores.
Així un quadrat de costat 1,
tindrà una diagonal que mesura V¯2¯
(arrel quadrada de 2)
A partir d'aquí podem deduir
que la diagonal d'un quadrat de costat n mesura: d
=n · V¯2¯
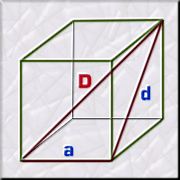
Si ara volem
calcular la mesura de la diagonal d'un cub, entre dos vèrtexs
de cares oposades, també podrem aplicar el Teorema de Pitàgores
si triangularitzem el cub i observem el triangle rectangle
format per una aresta inferior a,
la diagonal de la cara lateral d
i la diagonal gran D.
Així observarem
que D² = a² + d²
En el cas del cub d'aresta a = 1
la diagonal lateral d = V¯2¯
i, per tant:D² = 1² + (V¯2¯)²
= 1 + 2 = 3 => D = V¯3¯
- Òbviament podrem afirmar que la diagonal gran d'un cub de costat n
amida: D =n · V¯3¯
- Amb tot això, i si seguim aquest procediment de triangularització, podríem
calcular quant mesuren les diagonals de figures geomètriques de més
de 3 dimensions, és a dir, de figures que no existeixen, ni podem tampoc
imaginar donada la nostra limitació tridimensional.
La diagonal
gran d'una figura del tipus d'un cub, però de 4 dimensions, serà: D
= n · V¯4¯ = 2n
La diagonal gran d'una figura del tipus d'un cub, però de 5 dimensions, serà: D
= n · V¯5¯, etc.
- És magnífic poder calcular quelcom que no podem ni tan sols imaginar la seva forma! Em meravella que una ciència com les matemàtiques
pugui arribar on no ho fa ni la imaginació!
Com m'agradaria arribar a un món quadridimensional i demanar als seus habitants que m'ensenyessin
un dau i observar aquest objecte en què la seva diagonal mesura el doble que les seves arestes...
SOLUCIONS:
54² =
2.916 (2.500
+ 104 x 4 = 2.916)
41²
- 26² = (41 + 26) x (41 - 26) = 67 x 15 = 1.005
35² = 1.225
(3 x 4 = 12, 25)
41² = 1.681 (4²
= 16, 4 x 2 = 8, 1)
32² = 1.024 (3²
= 9, 3 x 2 x 2 = 12, 2² = 4) >> 9 +1 = 10, 2, 4 >> 1.024
75² = 5.625 (7
x 8 = 56, 25)
59² = 3.481 (6²
= 36, 6 x 2 = 12, 1) >> 360 - 12 = 348, 1 >> 3.481
115² = 13.225 (11 x 12 =
132, 25)
29 x 21 = 25² - 4² = 625 - 16 = 609
35 x 30 = 1.050 (no)
18 x 12 = 15² - 3² = 225 - 9 = 216
23 x 31 = 27² - 4² = 729 - 16 = 713
37 x 32 = 1.184 (no)
54 x 46 = 50² - 4² = 2.500 - 16 = 2.484
Extracte de la pàgina http://www.xtec.es/~bfiguera/curioso.html#quadrat
Autor: Blai Figueras Álvarez
 Un aspecte interessant dels
nombres
al quadrat és la "pèrdua" que es produeix si augmentem i disminuïm els nombres en una quantitat constant, és a dir, la diferència d'àrea entre
quadrats i rectangles amb un mateix perímetre.
Un aspecte interessant dels
nombres
al quadrat és la "pèrdua" que es produeix si augmentem i disminuïm els nombres en una quantitat constant, és a dir, la diferència d'àrea entre
quadrats i rectangles amb un mateix perímetre.
 El gran Pitàgores de Samos ens va llegà el seu arxiconegut Teorema
dels triangles rectangles, pilar fonamental de càlculs
geomètrics i trigonomètrics, en què es relacionen les
mesures dels catets i de la hipotenusa: a²
= b² + c²
El gran Pitàgores de Samos ens va llegà el seu arxiconegut Teorema
dels triangles rectangles, pilar fonamental de càlculs
geomètrics i trigonomètrics, en què es relacionen les
mesures dels catets i de la hipotenusa: a²
= b² + c²
