
7.- Si cada elemento de una línea de una matriz cuadrada se escribe como suma de dos sumandos, el determinante de dicha matriz es igual a la suma de dos determinantes que tienen iguales todas las líneas, excepto la línea de la descomposición, en la que el primer determinante tiene el primer sumando de cada elemento del inicial y el segundo determinante tiene el segundo sumando.
| Ejercicio:
Invéntate una matriz cualquiera y aplica la propiedad
anterior, buscando, preferiblemente, descomponerlas en
dos matrices más simples, es decir, que tengan alguna
línea paralela igual a otra o proporcional. Comprueba
los resultados.
|
8.- Si una línea de una matriz cuadrada es combinación lineal de dos o más líneas paralelas a ella, entonces, el determinante de la matriz vale 0.
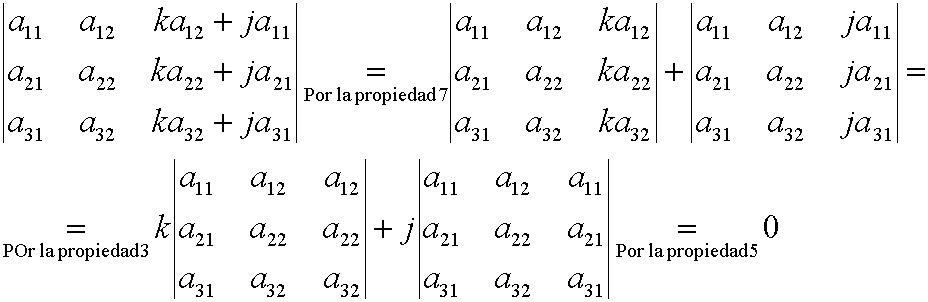
| Ejercicio:
Escribe en tu libreta un ejemplo de la misma propiedad en
la que se hayan modificado las filas en lugar de las
columnas, y resuélvelo. |
9.- El determinante de una matriz cuadrada no cambia si se le suma a una línea cualquiera una combinación lineal de otras líneas paralelas a ella.
| Ejercicio:
En un matriz cualquiera de las generadas aleatoriamente,
realiza los cambios siguientes y anota en tu cuaderno
qué cambios modifican el valor del determinante y qué
cambios no lo modifican: (F=fila C=columna)
|
10.- Todo determinante de una matriz cuadrada se puede convertir en otro del mismo valor que el dado, tal que todos los elementos de una línea, previamente elegida, sean cero excepto uno de ellos.
Ejemplo:
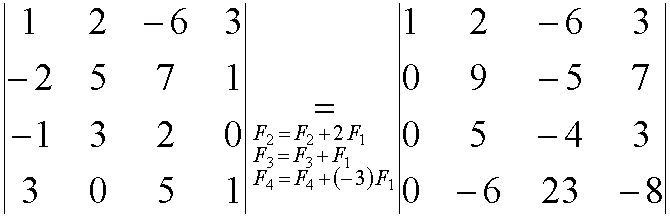
| Ejercicio:
Aplicando la propiedad anterior, diagonaliza (es decir,
haz cero todos los elementos menos la diagonal principal)
la matriz que aparece debajo. De la misma forma,
triangula (es decir, sólo haces cero los valores por
debajo de la diagonal) la matriz anterior (o cualquier
otra). Si alguno de los elementos de la diagonal
principal es cero, recuerda que puedes cambiar dos filas
o columnas variando sólo el signo del determinante. Por
ello, puedes cambiar dos veces para no variar el signo y
conseguir un elemento distinto de cero en la diagonal
principal.
|
11.- El determinante de una matriz triangular o diagonal es igual al producto de los elementos de la diagonal principal.
| Fernando Villarrubia Gahete | ||
 |
Ministerio de Educación, Cultura y Deporte. Año 2003 |