
página principal -----------asíntotas horizontales------------- asíntotas verticales
ASÍNTOTAS OBLÍCUAS
DEFINICIÓN
Una recta de ecuación y = mx + n (m¹0) es asíntota oblícua de una función f(x) si
|
INTERPRETACIÓN GRÁFICA
ESCENA 1
En esta escena tienes representada una función f(x) (en rojo) y su asíntota oblicua (en verde).
Comprueba que al dar valores grandes (en valor absoluto) a "x" la diferencia entre la gráfica de f y la asíntota es cada vez menor.(usa las flechas de colores para dar valores a "x")
ESCENA 2
CÁLCULO DE LAS ASÍNTOTAS OBLICUAS
1ª PARTE: Cálculo de la pendiente "m"
ECUACIÓN DE LA ASÍNTOTA:---- y = mx + n
ECUACIÓN DE LA FUNCIÓN: -----y = f(x)
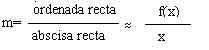
Esto quiere decir que "m" es un valor muy próximo al cociente entre f(x) y x, cuando x toma valores grandes (en valor absoluto). Por tanto, para calcular "m" hallaremos el siguiente límite
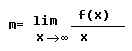
Comprueba que esto es así en la siguiente escena. Puedes cambiar los valores de "x" con las flechas de colores de la parte inferior.
| Observa que, para que exista ASÍNTOTA OBLICUA , "m" debe ser un número real distinto de cero. |
2ª PARTE: Cálculo de la ordenada en el origen "n"
ECUACIÓN DE LA ASÍNTOTA:---- y = mx + n
ECUACIÓN DE LA FUNCIÓN: -----y = f(x)
Después de calcular "m" es fácil
hallar el valor de "n". Fijándote en la definición
inicial, se cumple que ![]() . Operando se obtiene que "n" tomará el
valor
. Operando se obtiene que "n" tomará el
valor 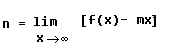
ESCENA 3
Ahora que ya sabes calcular las ASÍNTOTAS OBLICUAS de una función, practica con las que se te proponen a continuación:
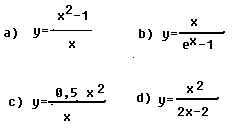
En la escena puedes dibujar, tanto la función (su ecuación en rojo) como sus asíntotas (su ecuación en verde).
AUTORA: Pilar García Freire