|
Pythagoras
of Samos (580-500 B.C.): Pythagoras, who lived some 50
years after Thales, was a more mysterious character who also
travelled in his youth to Egypt, Babylon and possibly India. It was in
these countries where he acquired and developed his knowledge of
mathematics and philosophy. He was a contemporary of Buddha, Confucius and
Lao-Tze which perhaps explains his interest in religious mysticism. He is
said to have been vegetarian which was common amongst believers in the
transmigration of souls. He settled at Croton, in southeast Italy, which
was part of Greece at that time, where he set up a secret sect called the
Pythagoreans, which helped the development and extension of mathematical
knowledge within the Hellenic world. Proclus (410-485 A.D.) also provides
the first written reference of Pythagoras in his "Commentary on the
First Book of Euclid's Elements". Immediately following on from his
writings on Thales he says of Pythagoras "(He) transformed this
science into a liberal form of education, examining its principles from
the beginning and probing the theorems in an immaterial and intellectual
manner. He discovered the theory of proportionals and the construction of
the cosmic figures". The Pythagoreans were the first scholars who
were more inspired by their love of wisdom and beauty than by practical
questions. It is difficult to separate history and legend when talking
about Pythagoras the man but there is not doubt that the Pythagorean
school played an important role in the development of ancient Greek
mathematics. Let us now have a closer look at some of his most important
discoveries:
|
|
The
expressions 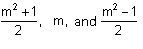 were
used to obtain Pythagorean triads, although they had already been
discovered by the Babylonians. were
used to obtain Pythagorean triads, although they had already been
discovered by the Babylonians.
They were
believed to be used to prove Pythagoras' theorem,
which the Babylonians were also conscious of but for which no proof had
been demonstrated up until this point in time. In this window you can see
a demonstration which makes use of similar triangles and segments which
are in proportion.
|




