Babylonian civilisation developed in the region between the Tigris and Euphrates rivers from the end of the fourth millennium before Christ. The empire lasted until the city of Babylon fell to Persia in 538 B.C. The Sumerians, who belonged to the culture, had developed a writing system (the cuneiform script) which was later discovered on thousands of ceramic tablets, unearthed during archeological excavations at Uruk. The script dates back to more than 5,000 years ago. After the Akkadian conquest, which took place during the third millennium before Christ, the Akkadians adopted the Sumerian form of writing and developed a positional number system. In other words, the value of a figure depended on its position within a number. The system they used was base sixty, which is still used today to measure time and angles. The table below highlights the mathematical developments that were made during the Babylonian civilisation.

Cuneiform script		Right: Tablet with pre-cuneiform script. The tablet appears to have been engraved using a cylindrical writing tool. Left: an example of cuneiform script. The writing tool used in this case is a triangular prism.
Number theory	Positional numeration in base 60 Sexagesimal fractions Fundamental operations which included working out square roots Number tables: for multiplication, reciprocals, squares, cubes, square and cubic roots, successive powers of a given number (the first logarithms) Pythagorean Triads Linear interpolation
Algebra	Linear equations Linear equation systems Quadratic equations Some cubic equations
Geometry	The area of flat shapes The volume of the frustum of a cone or pyramid Right-angled triangles The altitude of an isosceles triangle bisects the base Using the length of a chord in a circle of a given radius to find the apothem

(1900 to 1600 B.C.)

 There are many records of Babylonian script on clay tablets like the one in the photograph. A triangular prism-shaped implement was used to write in the soft clay, which was later baked in the sun or in ovens. Different impressions were made depending on the position of the prism and combinations of these impressions represented different words or numbers.

 These tablets have survived the passing of time well and thousands of tablets have been found at different archeological sites. By the end of the XIX^th century the discovery of a set of war chronicles written in three languages (Persian, Elamite and Babylonian) allowed the script to be translated into other languages. However, the mathematical content of the tablets was not deciphered until the XX^th century, thanks to the work of Thureau in France and Neugebauer in Germany and the United States.

Above: An illustration of a scribe's hand writing on a clay tablet with a reed.

Right: a number written in sexagesimal notation.

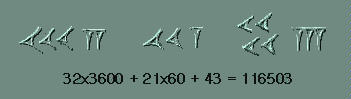Before 1700 B.C. the Babylonians had devised positional numeration in which the value of each figure depends on its position in the number. They had also devised the sexagesimal system in base 60, where each big unit is made up of 60 smaller ones. The system uses two basic symbols; the vertical symbol to represent units and the horizontal symbol to represent tens. By using a combination of these symbols, they could write the first 59 numbers. The number zero was not used until the year 400 B.C. and was represented by two symbols placed side by side obliquely. The number 59 is represented below using these symbols. For numbers higher than 60, e.g. the number 116,503 which is illustrated above, successive divisions are used where the number and its remainders are divided by 60. These remainders were then used to represent the number.

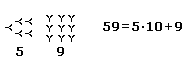
The Babylonians also used this system to represent sexagesimal fractions, i.e. successive powers of 60 in the denominator. They worked in the same way as our modern-day decimal units and they could therefore make calculations such as 2·60^-1+3·60^-2  One of the Old Babylonian tablets from the Yale Collection includes the calculation of the square root of 2 to three sexagesimal "decimal" places. In our notation the number would be written as 1;24,51,10 which is equal to 1+24/60+51/3600+10/216000=1.4144028, where the three first decimal numbers are accurate.

A first approximation of this root, a1, is chosen.

A second approximation is then obtained by finding the arithmetic mean of a1 and the equation a/a1=b1. Therefore, a2=(a1+b1)/2 which is a closer approximation.

This procedure can be referred to as an iterative algorithm which can continue indefinitely. Each stage gives a better approximation than the previous one.

Amongst the lists of numbers discovered were some triples (triads) of numbers such as the formulae p²-q², 2pq and p²+q^{2 .} These triads were used to construct right-angled triangles with different numbers and they found 38 pairs of values where p is less than 60 (Pythagorean triads). The first 15 triples can be found on the Plimpton tablet No. 322 at Columbia University.

We have used the formula C=Co·(1+r)^t which gives us 2=1·(1+20/100)^t and therefore 2=1.2^t. In order to find t we use logarithms, so t=log 2/log 1.2=3.801784. Remember that t is the exponent which the base number 1.2 needs to be raised to in order to get the answer 2 (the definition of a logarithm of 2 in base 1.2).

In Mesopotamian culture (1+20/100) corresponded to the cuneiform number 1;12. One problem was to find out to what power a certain number must be raised to get the answer 2. Two powers are chosen, one greater than and the other less than 2 which give the answers (1;12)³ = 1;43,40 and (1;12)⁴=2;4,25 respectively. Using the rule of three the scribe got the answer 3;47,13,20 years, which is 3.787. Logarithms on modern-day calculators give us the number 3.802.

In the following window you can see how a linear interpolation  problem is represented on a graph.

The graphical solution to the problem is found by locating the point on segment PQ which corresponds to the relevant y-coordinate, as is still done nowadays. The data is recorded in the table below. Some of the numbers are written using sexagesimal notation. You can solve the same problem using different data by changing the position of points P and Q and tripling or multiplying the capital by another number.

The Babylonians used many formulae which gave fairly accurate results to work out area and volume. They calculated the area of a quadrilateral by taking the product of the arithmetic means of the pairs of opposite sides. The volume of a frustum of a cone or a pyramid was found by taking the arithmetic mean of the area of the bases. The following formula was used to calculate the area of the pyramid frustum accurately:

We have already mentioned how the Plimpton tablets showed evidence that Pythagoras' theorem was used. Evidence of working with similar shapes was also found in a collection at Susa.

().

2.-The table below shows some of the data recorded in sexagesimal notation, on tablets found at Susa, 300km from Babylon:

Even 4,000 years ago they were able to solve all quadratic equations which had positive roots. The existence of equations with negative roots wasn't even considered until the modern period. Up until this point quadratic equations had always fallen into three groups and the Babylonians were able to solve them using operations such as multiplying the whole equation by a number. These operations are present in problems such as: find the side of a square if the side taken away from its area is 14;30. The solution given is:

"Take half of 1, which is 0;30, and multiply 0;30 by 0;30, which is 0;15; add this to 14;30 to get 14,30;15. This is the square of 29;30. Now add 0;30 to 29;30, and the result is 30, the side of the square".

They then used their square or roots tables to find the root of 14,30;15.

If the equation was in the form ax²+bx=c, then it could be solved by multiplying it by "a", to obtain (ax)²+b(ax)=c and then finding "ax" to determine the value of "x". This is one of the first examples of substituting an unknown to solve equations and was an outstanding discovery for the early Babylonians.

One of the most frequently used tables in Babylonian algebra was that of the values of n³+n²  where "n" is a natural number. These tables were used to solve cubic equations in the form: x³+x²=a . If there were any other coefficients in the equation other than 1 then the equation was changed by completing the cube and substituting an unknown quantity in the same way as was done with quadratic equations. Therefore, the equation ax³+bx²=c was multiplied by a²/b to get ax/b.

This method of substituting an unknown in an equation allowed the Babylonians to solve some equations of the 4^th or 8^th power, which are referred to these days as biquadratic equations.

Tablet 322 illustrated in the photo above contains lists of numbers which are arranged in columns. These numbers appear to indicate the possible sides of right-angled triangles (Pythagorean triads) together with other information about these triangles. The numbers on the tablet fit into the following formulae:

The rows are arranged so that the numbers decrease from top to bottom according to the ratio a/b, which corresponds to the modern day trigonometric ratio secant C. The first column on the left is a table of values of sec² A which starts with sec² 45º and ends with sec² 31º. However, the tablets do not contain any data which resembles modern day angle measurement as the Babylonians probably preferred to work with ratios of segments. 

It is highly likely that these ratios were used to construct different shaped right-angled triangles.