
CÁLCULO DEL NÚMERO ÁUREO
El número áureo F es un número irracional, para obtenerlo procedemos de la siguiente manera:
Dado el
segmento 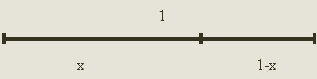
obtenemos la siguiente proporción:
(I) ![]()
resolviendo la ecuación de segundo grado, obtenemos:

la solución con la raíz negativa no es valida y como F es la razón de la proporción (I), tenemos que F =1/x= 1,6180033988, al número 0,618033988 se le llama número áureo unitario y se le representa por la letra griega d.
En la página anterior obtuviste dos números como razones: 1,618 y 1,617, esto es debido a que solo se usan dos o tres decimales para los cálculos.
CURIOSIDADES
Tanto el número áureo F como el número áureo unitario d han tenido una enorme importancia cultural y estética en la historia, aparecen en:
Edificios (Partenón, Monasterio del Escorial)

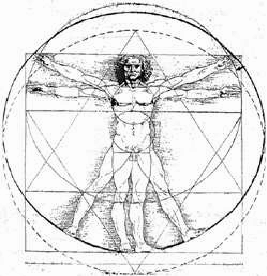
Obras de arte (en el canon de Leonardo el radio del círculo es la sección áurea de la altura del individuo, es decir, de la altura del cuadrado)
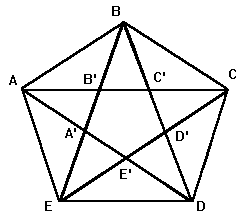
Figuras geométricas (en el pentagrama o estrella de cinco puntas AB' es la sección áurea de AC' que a su vez es la sección áurea de AC)
El número áureo F también aparece en la sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, .... puedes comprobar que an/an-1 tiende a F.
Autor: José Luis Triguero Grueso
| Alumno | |
| Ministerio de Educación, Cultura y Deporte. Año 2000 | |
| Alumno |