Lugares geométricos

Aquí el alumno se va a encontrar con:

-Una presentación (pseudomágica) del tema, utilizando el lugar de los puntos que equidistan de otros dos puntos fijos.

-Estudio de óvalos y lemníscatas.

-Estudio de la cisoide.

-Estudio de cicloides alargadas y acortadas.

-Estudio de hepicicloides e hipocicloides.

-Estudio de hepicicloides e hipocicloides alargadas y acortadas: esta última parte puede considerarse como la continuación de la anterior. Las últimas actividades (24 y 25) son realmente avanzadas y de profundización.

Presentación:

Por lugar geométrico entenderemos el conjunto de puntos que satisfacen una determinada condición.

Empecemos por averiguar el lugar geométrico de los puntos que equidisan de dos puntos A y B. Para ello sigue los siguientes pasos:

a.-Limpia la pantalla de la siguiente escena, pulsando el botón que se halla en la parte inferior derecha, llamado "limpiar". Si es la primera vez no es necesario ya que la escena inicialmente no tiene ningún rastro. Si no ves el punto P pulsa la tecla que se halla en la esquina inferior izquierda, llamada "inicio".

b.-Arrastrar con el ratón los puntos A y B a la zona de la escena que desees. Si es la primera vez puedes omitir este paso.

c.-Sitúa el cursor sobre el punto P, pulsa el botón izquierdo del ratón y no lo sueltes. (Acabas de convertir al ratón en una varita mágica que, al moverla ordenará al punto P que se mueva sólo a través de los puntos que constituyen el lugar geométrico que nos interesa.) Sin sortarlo, mueve el ratón de un sitio a otro, intentando barrer toda la pantalla con el cursor. Procura no perder de vista el movimiento del punto P y cuida de que no se salga de la escena. Notarás que el punto P sólo se mueve por una zona concreta de la pantalla, dejando un rastro. En efecto, el punto P se mueve solamente por los puntos del lugar geométrico, marcándolos. De esta manera puedes reconocer la forma del lugar geométrico.

d.-¿Qué forma tiene el lugar geométrico de los puntos que equidistan de A y B?¿Crees que, si varías las posiciones relativas de los puntos A y B, cambiará la forma? Compruébalo empezando desde el primer paso.

Por supuesto, en ésto no hay magia ninguna. Se trata de ordenarle al punto P que se mueva a lo largo de la línea recta cuya ecuación es

(B.x-A.x)*x+(B.y-A.y)*y-(B.x^2-A.x^2+B.y^2-A.y^2)/2=0

ya que sabemos de antemano que el lugar geométrico de los puntos que equidistan de A y B es la mediatriz del segmento que une los puntos A y B, cuyas coordenadas son, respectivamente (A.x,A.y) y (B.x,B.y).

A veces no es tan fácil adivinar de antemano cual es el lugar geométrico asociado a una condición impuesta. Vamos a estudiar algunos casos que no son nada intuitivos.

Óvalos y lemníscatas

Estudiemos el lugar geométrico de los puntos del plano tales que el producto de sus distancias a dos puntos fijos F y G (llamados focos), es una constante b^2.

Llamando 2*a a la distancia entre los focos F y G; y situando ambos en el eje de abscisas de tal manera que equidisten del origen de coordenadas, las coordenadas cartesianas de los focos son F=(-a,0) y G=(a,0). Llamamos a las coordenadas de cualquier punto P del lugar geométrico (x,y).

La distancia entre P y F es la raiz cuadrada de ((x+a)^2+y^2); y entre P y Q es la raiz cuadrada de ((x-a)^2+y^2). El producto de ambas ha de ser constante e igual a b^2. Elevamos al cuadrado ambos miembros de la ecuación con el fin de eliminar las raices cuadradas. Se obtiene:

((x+a)^2+y^2)((x-a)^2+y^2)=b^4

Se denomina óvalo de Cassini al lugar geométrico representado por esta ecuación.

1.-A continuación experimenta como varía su forma al variar los parámetros a y b.

2.-Dibuja en tu cuaderno la figura que se obtiene para cada uno de los casos a<b, a=b y a>b.

Cuando a=b, el origen es un punto del óvalo, que adquiere forma de ocho. Se denomina entonces Lemníscata.

Cisoide

Para construir la cisoide se necesita una circunferencia y una recta tangente a ella. Veamos la siguiente figura.

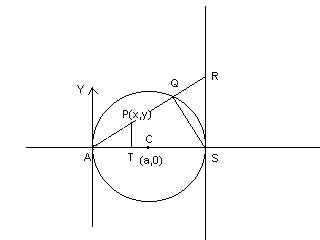
El punto de tangencia es S y A es el diametralmente opuesto. Hemos situado el origen de coordenadas en A, de tal manera que el centro C de la circunferencia tiene de coordenadas (a,0), donde a es precisamente el radio. Consideremos un punto R sobre la recta, que pueda moverse libremente sobre ella. El segmento AR corta a la circunferencia en el punto Q. Se ha elegido un punto P, de coordenadas (x,y), sobre el segmento AR que cumple la condición de estar a la misma distancia de A que Q de R. Si llamamos AP a la primera distancia y QR a la segunda, entonces se cumple que AP=QR. El segmento PT es paralelo al eje Y, estando el punto T en el eje X. Este segmento y el QS se utilizarán después para obtener la ecuación de la cisoide.

Cuando el punto R se desplaza por la recta el segmento AR cambia su orientación moviéndose el punto Q sobre la circunferencia, y el punto P sobre el segmento AR para que se cumpla la condición AP=QR.

¿Cuál es el lugar geométrico de los puntos P?

Para verlo aplicamos el teorema de Pitágoras al triángulo AQS, QS^2=AS^2-AQ^2=4a^2-AQ^2=4a^2-(AR-QR)^2=4a^2-(AR-AP)^2

Observemos ahora que los triángulos ATP y ASR son semejantes, por lo que AR=(2a/x)*AP

También nos fijamos en que AP^2=x^2+y^2, por lo que tenemos

QS^2=4a^2-((2a/x)*AP-AP)^2=4a^2-((2a/x)-1)^2*AP^2=4a^2-((2a/x)-1)^2*(x^2+y^2)

Por otro lado, si aplicamos el teorema de Pitágoras al triángulo SQR tenemos que QS^2=RS^2-QR^2=RS^2-AP^2

De la semejanza de los triángulos ATP y ASR también podemos obtener que RS=2ay/x

Obtenemos ahora que QS^2=(2ay/x)^2-(x^2+y^2)

Si igualamos las dos expresiones que se han obtenido para QS^2 obtenemos finalmente la ecuación cartesiana de la cisoide:

x^3+xy^2-2ay^2=0

3.- Para obtener la forma de esta curva procede de la siguiente manera: con el ratón agarra el punto R de la siguiente escena y muévelo, lentamente, a lo largo de la recta cuya ecuación es x=2*a. El punto P se desplazará, dejando el rastro que nos interesa. Para obtener una visión más amplia puedes disminuir la escala, por ejemplo hasta el valor 20, y repetir el proceso.

4.-Dibuja la gráfica en el cuaderno y al lado escribe su ecuación. ¿Crees que la curva cortará alguna vez a la recta? Sigue al punto P ampliando la escala cuando lo necesites y desplazando hacia abajo el origen de coordenadas (aumenta para ello el valor de Oy). Aunque al hacer esta operación se pierda el rastro, no te preocupes porque lo que nos interesa es ver si el punto P está a la derecha o a la izquierda de la recta, nada más. Anota tus conclusiones.

5.-Comprueba que las coordenadas del punto P que aparecen en la escena satisfacen la ecuación de la cisoide. Elige, para ello cuatro posiciones distintas y compruébalo en las cuatro.

Cicloides alargadas y acortadas

Una cicloide acortada es la curva engendrada por un punto P en el interior de un círculo que rueda sin deslizar por una recta. Si el punto P es exterior al círculo móvil, se denomina cicloide alargada.

Supongamos que el círculo rueda sobre el eje X, sin deslizar. Inicialmente la situación es tal que: 1) el círculo tiene a su izquierda al eje Y y lo toca tangencialmente; 2) el punto P yace justo debajo del centro C de la circunferencia, a una distancia a de ésta. El número a es negativo si P está en el interior del círculo, cero si está sobre la circunferencia y positivo si está fuera.

Las coordenadas del centro C son (r+r*cos(m),r), en donde r es el radio de la circunferencia y m el ángulo que ha rodado la misma.

Las coordenadas del punto P vistas desde el centro de la circunferencia son (-(r+a)*sen(m),-(r+a)*cos(m)). Las coordenadas (x,y) del punto P, vistas desde el origen de coordenadas O, son la suma de las coordenadas del centro más las coordenadas del punto P vistas desde el centro, es decir:

x=r+r*m-(r+a)*sen(m)

y=r-(r+a)*cos(m)

6.-En la siguiente escena agarra, con el ratón, el centro C y desplázalo hacia la derecha. El círculo rueda sobre el eje X. El punto P dibuja una cicloide alargada porque a>0. Si deseas ver más ciclos disminuye la escala.

7.-Para ver la forma que tienen las cicloides acortadas hay que cambiar el valor de a, haciendo que sea menor que 0 pero mayor que -r (en este caso r=1) para que el punto P esté dentro del círculo.

Para ello hacer click sobre el botón "config" que está en la esquina superior derecha. Nos aparece la ventana de configuración de la escena. Pulsar el espiner (triangulito pequeño de color negro) que hay a la derecha de la palabra <applet>, para que se despliegue un menú. Señalar la opción "auxiliares" y hacer click. Aparecen los auxiliares definidos en esta escena. En la segunda línea aparece definido el auxiliar a con un valor 0.5. Cambiarlo por otro valor cualquiera que sea menor que 0 y mayor que -1, por ejemplo -0.5. No hay que tocar lo demás. (Si nos equivocamos y no recordamos la configuración inicial podemos hacer click sobre el botón "original", que está justo a la izquierda del botón "prueba", y de esa manera nos devuelve los valores iniciales de la configuración, pudiendo empezar de nuevo.) A continuación pulsar la tecla "prueba" que se halla arriba a la derecha, justo al lado de la palabra <applet>. Esto nos va a permitir probar el funcionamiento de la escena con el nuevo valor de a que hemos seleccionado. El punto P aparece ahora dentro del círculo y vemos también actualizado el valor de a. Si deseamos probar otro valor repetiremos los pasos volviendo a pulsar el espiner.

8.-Dibuja en tu cuaderno las cicloides alargadas y acortadas para los valores a=0.8, a=-0.2.

9.-¿Cómo es la cicloide cuando a=0? Compruébalo en la escena cambiando el valor de a. Dibújala en tu cuaderno. En este caso es interesante señalar que la velocidad de P, respecto del origen O, en los puntos de contacto con el eje X es cero, ya que el punto P pasa de caer a subir de forma continua en esos puntos.

10.-Comprueba que las coordenadas del punto P satisfacen las ecuaciones dadas arriba. Utiliza cuatro puntos distintos y sus respectivos valores del ángulo m, para un a fijo. Anota los resultados en tu cuaderno.

Epicicloides e hipocicloides

La curva engendrada por un punto P de una circunferencia de radio r, que rueda sin deslizar por otra circunferencia de radio R (R mayor o igual que r) se llama hipocicloide, si ambas circunferencias están al mismo lado de la tangente común, y epicicloide si están a distinto.

Consideremos la siguiente figura en la que R y r son los radios de las circunferencias grande y pequeña respectivamente. Tomemos como situación inicial aquella en la que coinciden en el eje X, el punto P, el punto de tangencia M y el punto Mo (punto de tangencia inicial); es decir que P inicialmente es un punto de tangencia.

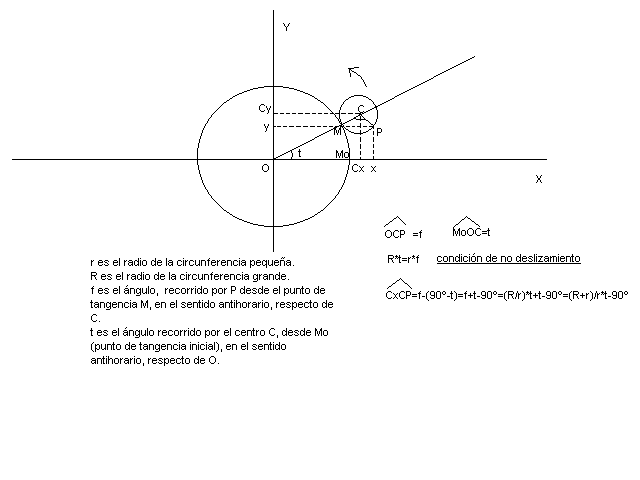
La ecuaciones paramétricas de las epicicloides pueden obtenerse de la siguiente manera:

Las coordenadas (x,y) del punto P se obtienen de la figura y son

x=Cx+r*sen((R+r)/r*t-90º)=Cx-r*cos((R+r)/r*t)

y=Cy-r*cos((R+r)/r*t-90º)=Cy-r*sen((R+r)/r*t)

Si tenemos en cuenta que Cx=(R+r)*cos(t) y Cy=(R+r)*sen(t), obtenemos

x=(R+r)*cos(t)-r*cos((R+r)/r*t)

y=(R+r)*sen(t)-r*sen((R+r)/r*t)

Si repetimos los mismos pasos para obtener las ecuaciones de la hipocicloide veremos que las ecuaciones son muy parecidas. Podemos escribir de forma compacta las ecuaciones de las epicicloides e hipocicloides, utilizando un parámetro e, que vale +1 para las epicicloides y -1 para las hipocicloides:

x=(R+e*r)*cos(t)-e*r*cos((R+e*r)/r*t)

y=(R+e*r)*sen(t)-r*sen((R+e*r)/r*t)

El punto P puede no estar sobre la circunferencia pequeña y hallarse más o menos alejado del centro de ella. Utilicemos otro parámetro a que mida este hecho. Si P está sobre la circunferencia pequeña entonces a=0. En general, a será la distancia de P a esa circunferencia, siendo positivo si está fuera y negativo si está dentro. Las ecuaciones tras esta generalización son:

x=(R+e*r)*cos(t)-e*(r+a)*cos((R+e*r)/r*t)

y=(R+e*r)*sen(t)-(r+a)*sen((R+e*r)/r*t)

Estas son las ecuaciones paramétricas de las epicicloides (e=+1) e hipocicloides (e=-1), alargadas (a>0) y acortadas (a<0).

Realicemos un seguimiento interactivo del punto P para ver como se originan estas curvas.

11.-En la escena que sigue pulsar el botón "config" (queremos fijar los valores de los parámetros R, r, e y a). Seleccionar "auxiliares". Comencemos con una epicicloide (e=+1) alargada (a=0.5), tomando R=1 y una relación de radios R:r, 2:1, es decir R es el doble que r (por tanto r=0.5) y pondremos k=2, en donde k=R/r. El valor de r no es necesario escribirlo porque con los valores de R y k es suficiente. Así pues, tecleamos R=1, k=2, e=+1 y a=0.5. Puede ocurrir que algunos de estos valores ya estén escritos y no necesitemos teclearlos de nuevo. No tocar nada más. Si, por error, hemos cambiado algo y no recordamos sus valores iniciales, pulsaremos el botón "original" para recuperar la configuración de partida y así poder empezar otra vez. ¡Alto, no empieces aún! Sigue leyendo.

Después de cambiar los parámetros en el apartado "auxiliares" tenemos que hacer click sobre el triangulito que nos despliega el menú, y seleccionaremos ahora "controles". Aparece un corchete y en su interior dos números separados por una coma. Son las coordenadas iniciales del centro C de la circunferencia pequeña. Observar que la ordenada es 0. Hay que cambiar el valor de la abscisa de tal manera que se cumpla siempre que sea igual a R+e*r. En este caso habrá que escribir 1.5. ¡Ahora puedes hacerlo!

A continuación pulsa el botón "prueba" para aceptar los cambios que hemos hecho. La nueva escena aparece con los parámetros actualizados.

12.-Colocamos el cursor sobre el centro C de la circunferencia pequeña, hacemos click con el botón izquierdo, y no lo soltamos. Arrastramos C concéntricamente a la circunferencia grande para que la circunferencia pequeña ruede sobre la grande. El punto P gira también, dejando un rastro que nos marca el lugar geométrico. Si forzamos a C a correr muy rápido nos saltaremos muchos puntos del lugar geométrico, por lo que conviene no tener mucha prisa. Si una zona no ha sido muy pintada podemos retroceder para que vuelva el punto P a pasar por ella.

13.-Anota y dibuja en tu cuaderno los parámetros y la curva obtenida en este caso.

14.-Experimenta, cambiando los valores de los parámetros. Recuerda que tienes que empezar pulsando el botón "config". Te recomendamos que no cambies el valor R, dejando R=1, ya que lo que importa es la relación R/r, es decir k. El parámetro a tiene que ser mayor o igual que -r. No olvides, después de cambiar los parámetros, cambiar también la abscisa del centro C, haciéndola igual al valor de R+e*r.

Procura que k sea siempre un número natural: 1, 2, 3, 4,..., etc. Si utilizas otro valor para k entonces la curva no se cerrará en una vuelta y necesitarás más vueltas. Pero ésto, la escena no lo sabe hacer, ya que aquí solamente se dibuja el resultado de la primera vuelta, nada más. Si quieres ver el resultado de la segunda vuelta (nada más) tienes que sumar 2*pi al ángulo t, que lo encontrarás en la herramienta "auxiliares". Si quieres ver el resultado de la tercera vuelta (nada más) sumarás 4*pi, de la cuarta sumarás 8*pi, etc. No olvides pulsar después el botón "prueba" para aceptar los cambios.

15.-Nefroide: es una epicicloide con k=2. En el apartado 11.- hemos visto un caso particular de nefroide alargada (a=0.5). Estudia los demás casos y dibújalos en tu cuaderno. Por ejemplo estudia los tres casos siguientes: 1) nefroide acortada (a=-0.2), 2) nefroide (a=0) y 3) nefroide alargada (a=0.5). Éste último ya lo has hecho.

16.-Cardioide: es una epicicloide con k=1. Se pide lo mismo que antes.

17.-Astroide: es un hipocicloide con k=4. Se pide lo mismo que antes.

18.-Deltoide: es un hipocicloide con k=3. Se pide lo mismo que antes.

19.- La elipse puede obtenerse como si fuera una hipocicloide acortada con k=2. Comprobar esta afirmación .

Epicicloides e hipocicloides alargadas y acortadas

En la siguiente escena podremos ver como es la evolución de una epicicloide o hipocicloide con respecto a la variación del parámetro a. Además ya no hay restricción sobre el tipo de valor que hay que asignar a k, aunque recomendamos empezar con valores naturales. En la parte inferior de la escena aparece editada la ecuación en paramétricas. El alumno que lo desee puede cambiar aquí los valores de los parámetros auxiliares, aunque recomendamos el método explicado en anteriores apartados, por ser más rápido.

Ahora ya no es necesario dar valores al parámetro a, ya que podemos variarlo, casi continuamente, utilizando los espiner que aparecen debajo, en la escena. El mínimo valor que puede tomar a es -r; y, para que así sea, tenemos que escribirlo. Para hacerlo, pulsamos el botón "config" y a continuación seleccionamos la herramienta "parámetros". La opción "min" ha de estar igualada a -r, para lo cual primero tenemos que calcular r (r=R/k).

Tampoco es necesario actualizar la abscisa del centro C, ya que en esta escena hemos preferido prescindir de ambas circunferencias, con el fin de que el alumno vea las curvas aisladamente.

20.-Nefroide: hacer k=2, R=1 y e=+1 utilizando el método habitual. La opción "min" del parámetro a habrá que igualarla a -0.5. Variar el parámetro , desde la escena, y observar lo que ocurre con la curva, especial mente en los casos a=R y a=0.

21.-Cardioide: hacer k=1, R=1 y e=+1. Variar a y observar como antes.

22.-Astroide: hacer k=4, R=1 y e=-1. Variar a y observar como antes.

23.-Deltoide: hacer k=3, R=1 y e=-1. Variar a y observar como antes.

24.-Experimentar con otros valores en que k sea un número natural.

Si deseamos aumentar la resolución con el fin de mejorar la calidad del dibujo de la curva tenemos que aumentar el número de iteraciones para pedirle al programa que calcule más puntos intermedios. Ésto, lógicamente ralentiza el programa. Para hacerlo pulsamos el botón "config" y seleccionamos la herramienta "curvas" (tendremos que utilizar la barra de desplazamiento vertical). Si leemos la linea (tendremos que utilizar la barra de desplazamiento horizontal) nos encontraremos con la instrucción "parametro=t[0,40*pi]10000". El número de iteraciones es 10000 y podemos aumentarlo o disminuirlo. Si decidimos aumentarlo a 20000 tendremos que sustituir el 10000 por el 20000. Después aceptamos el cambio pulsando el botón "prueba". Todo ésto será necesario, sobretodo si elegimos un valor grande para k.

25.-Experimentar con otros valores en que k sea un número racional.

Finalmente pedimos al alumno que tenga en su cuaderno un registro de todo lo hecho y que repase, si es necesario, los aspectos que no le hayan quedado aclarados.

Autor: Agustín del Pino Valero

	Ministerio de Educación, Cultura y Deporte. Año 2000