
PROPORCIONALIDAD
TEOREMA DE
THALES
Thales
de Mileto fue uno de los siete sabios de Grecia, vivió en el
siglo VI a. de C. enunció el teorema que lleva su nombre. En Egipto,
por encargo del Faraón midió las pirámides aplicando
el método de las razones de semejanza.
Figuras semejantes:
Dos figuras geométricas son semejantes cuando tienen exactamente
la misma forma. Difieren en sus dimensiones.
Segmentos homólogos:
Dos segmentos son homólogos cuando se corresponden en la semejanza.
Razón
de segmentos: Dados dos segmentos cualesquiera, llamamos razón
de dos segmentos a su cociente.
Razón
de semejanza: Llamamos Razón de semejanza al cociente que
se obtiene al dividir dos segmentos homólogos.
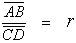
I
Teorema de THALES: Cuando un sistema de rectas paralelas
corta a dos rectas cualesquiera en un plano, los segmentos determinados
sobre una de ellas son proporcionales a los segmentos homólogos
obtenidos sobre la otra recta.
Modificando
el parámetro m obtenemos rectas que forman parte del
haz de rectas que pasan por el punto P.
Propuesta
de trabajo:
1.-
Observa que modificando el parámetro m,
se modifican todas las rectas y por consiguiente los puntos de corte: A,
A´, B, B´, C y C´. Determina a
partir de estos valores la longitud de los segmentos AA´, BB´,
CC´, AB, AC, BC, A´B´, A´C´ y B´C´.
2.-
En la parte superior derecha de la escena se han hallado las razones de
los segmentos: AB, A´B´ y BC, B'C'.
¿Es la misma razón para AC, A´C´?.
3.-
¿Comprueba si tienen la misma razón los segmentos: AA´,
BB´ y BB´, CC´.
TRIÁNGULOS
DE THALES
II Dos triángulos
se dicen de Thales o que están en posición de Thales, cuando:
Tienen un ángulo
común y los lados opuestos a dicho ángulo son paralelos.
4.-
El triángulo ABC se ha cortado por dos rectas DE
paralela a BC y EF paralela a AB,
obteniendose así los triángulos ABC, ADE
y CEF. Comprueba que modificando los valores del parámetro
m, se obtienen triángulos en posición de Thales.
III Dos triángulos
de Thales, sus lados, tienen la misma razón de semejanza
5.-
El ángulo BAC es común en los triángulos
BAC y DAE, también el ángulo
ACB es común en los triángulos ACB y
ECF, en cada caso los lados son paralelos.
Comprueba
que los lados de los triángulos semejantes, son proporcionales.
Observa
que al modificar m
se modifican los lados de los triángulos, con los nuevos valores
que aparecen como medida de los lados, comprueba que los lados siguen siendo
proporcionales (ten en cuenta que
con un solo decimal existen errores de cálculo en la aproximación
de la medida del lado)
Autor: Carlos
Pellicer Gorri
