
PUNTOS NOTABLES DE UN TRIÁNGULO
Incentro
El Incentro es el punto donde se cortan las tres bisectrices de un triángulo. Tiene la interesante propiedad de ser el centro de la circunferencia inscrita en el triángulo.
I.- Bisectriz de un ángulo
Un ángulo lo forman dos semirrectas con un origen común llamado vértice del ángulo. Para dibujar el ángulo fijaremos el vértice en el origen de coordenadas y uno de los lados lo hacemos coincidir con el eje positivo de las abscisas. Los ejes de coordenadas no van a estar visibles en las diferentes escenas.
Se llama bisectriz a la semirrecta que parte del vértice del ángulo y divide a éste en dos ángulos iguales.
Vamos a ver dibujada la bisectriz del ángulo.
¿Cómo se dibuja la bisectriz de un ángulo?
Observa esta secuencia de cuatro dibujos.
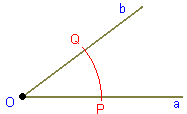
a) Con centro el vértice (O) del ángulo se traza un arco de cualquier radio que corta a los lados a y b en los puntos P y Q respectivamente.
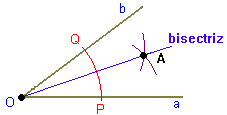
b) Centrando en los puntos P y Q, se trazan dos arcos de circunferencia del mismo radio que se cortarán en un punto A.

c) La semirrecta que une el vértice O con el punto A es la bisectriz del ángulo.
Actividades:
Cambiando la apertura del ángulo (que está expresada en grados), observa cómo cambia el dibujo de la bisectriz.
Dibuja en tu cuaderno las bisectrices de tres ángulos, uno agudo, otro recto y, el último, obtuso.
II.- Circunferencia tangente a los dos lados de un ángulo
Cualquier circunferencia que sea tangente a los dos lados del ángulo tiene su centro en la bisectriz.
Actividades:
¿Cómo dibujar una circunferencia tangente a los lados del ángulo?. Desde el centro que elijamos se traza la perpendicular a uno de los lados, que cortará a éste en un punto. El radio será la distancia entre el centro y el mencionado punto de corte.
III.- Las bisectrices de un triángulo
Las tres bisectrices interiores se cortan en un punto S, que se llama incentro.
(En los lados del triángulo aparece su longitud)
Actividades:
IV.- La circunferencia inscrita
El punto de corte de las bisectrices, obtenido en el apartado anterior, es el centro de la circunferencia inscrita.
Actividades: