PARALAJE

En esta unidad vamos a trabajar con el concepto de PARALAJE, con el fin de que lo conozcas y compruebes que con elementos geométricos sencillos, SEMEJANZA y RAZONES TRIGONOMÉTRICAS, podemos obtener datos de nuestro entorno, de gran importancia.

PARALAJE:

Es la medida angular, expresada en radianes, bajo la que se observa el radio de la órbita del planeta TIERRA, alrededor del SOL. Nota 1ª

Analiza la figura adjunta y responde:

El ángulo a =APB recibe el nombre de: ......................

El segmento AB es: .......................................................

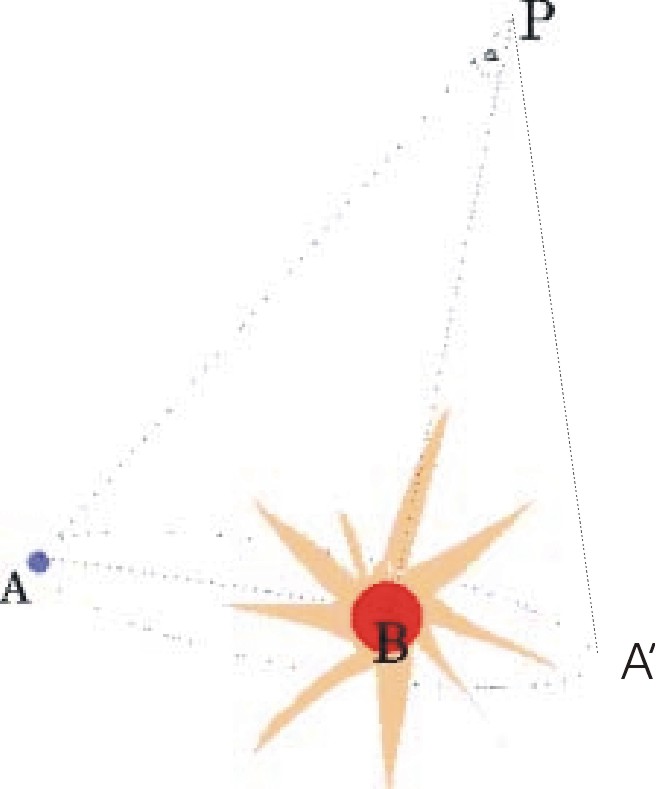
En el triángulo rectángulo APB, se verifica que:

tan a= AB/PB =a (expresado en radianes y para ángulos pequeños)

si a es igual a 1^”  y AB=1,5 10⁸Km (una U.A.),

halla PB

a (en radianes) = .........................................

ten presente que 360º = 2p radianes

NOTA: Analiza los conceptos expuestos en la escena siguiente, en la que se nos muestra la Tierra orbitando alrededor del Sol

*Podemos observar que para hallar el ángulo es suficiente con volver a posicionar la estrella en el telescopio y medir el ángulo formado con la posición anterior.

Consideramos el triángulo APA', en donde la distancia AA' es de 2U.A.

Analicemos, en esta escena, los valores que toman los elementos: tan a, a, PA y PA', (a=a) cuando nos alejamos del segmento AA' (diámetro orbital) alrededor de la línea de referencia (línea de color gris, a lo largo de la cual, el triángulo APA' es isósceles). Arrastra el punto P con el ratón.

NOTA: observar que, cuanto más lejos estamos del segmento AA', la oscilación de P alrededor de la línea de referencia es mayor, sin que se modifique el cociente de PA'/PA y el valor de a es igual al de la tan a

Podemos darnos cuenta que el cociente de las dos dimensiones es prácticamente uno, lo que señala que, a distancias grandes, las podemos considerar iguales o lo que es lo mismo, el triángulo es isósceles. 

Esto nos permite seguir considerando el triángulo como isósceles, aunque observemos estrellas que estén lejos de la vertical al Sol en el plano formado por la órbita terrestre (plano de la eclíptica).

Una vez que hemos calculado el ángulo de paralaje, calcular la distancia es muy sencillo, puesto que será:

distancia de la estrella al Sol = 1U.A./a radianes, si a=1''=0,000004848 radianes, recibe el nombre de PARSEC equivalente a 3,26 al (años luz)

Aparquemos por unos momentos lo expuesto y hagamos algunas reflexiones:

1º la Tierra no se desplaza solamente alrededor del Sol, sino que gira sobre si misma. Estos dos movimientos hacen que el posicionamiento del telescopio, junto con el movimiento de precesión (movimiento del eje de rotación del planeta), sea una operación compleja.

2º el sistema que solemos emplear, por ser más cómodo, es el fotográfico. Está basado en el cambio de posición aparente de un objeto frente a un fondo fijo.

Veámoslo:

Si observamos un objeto primero con un ojo y luego con el otro, vemos que éste se desplaza respecto a los objetos del fondo, analicemos este fenómeno a través del ejemplo siguiente, realizado con una cámara fotográfica ubicada en dos posiciones distintas:

En las dos tomas y en la superposición, que hemos realizado con un programa de tratamiento fotográfico,  podemos analizar lo que hemos comentado. Si observamos las fotos, podemos darnos cuenta que el muñeco situado sobre la mesa, parece que se ha movido respecto de la máquina de escribir, situada al fondo de la habitación.

Podemos darnos cuenta que el gráfico nos muestra la situación creada en la película de la cámara al superponer los negativos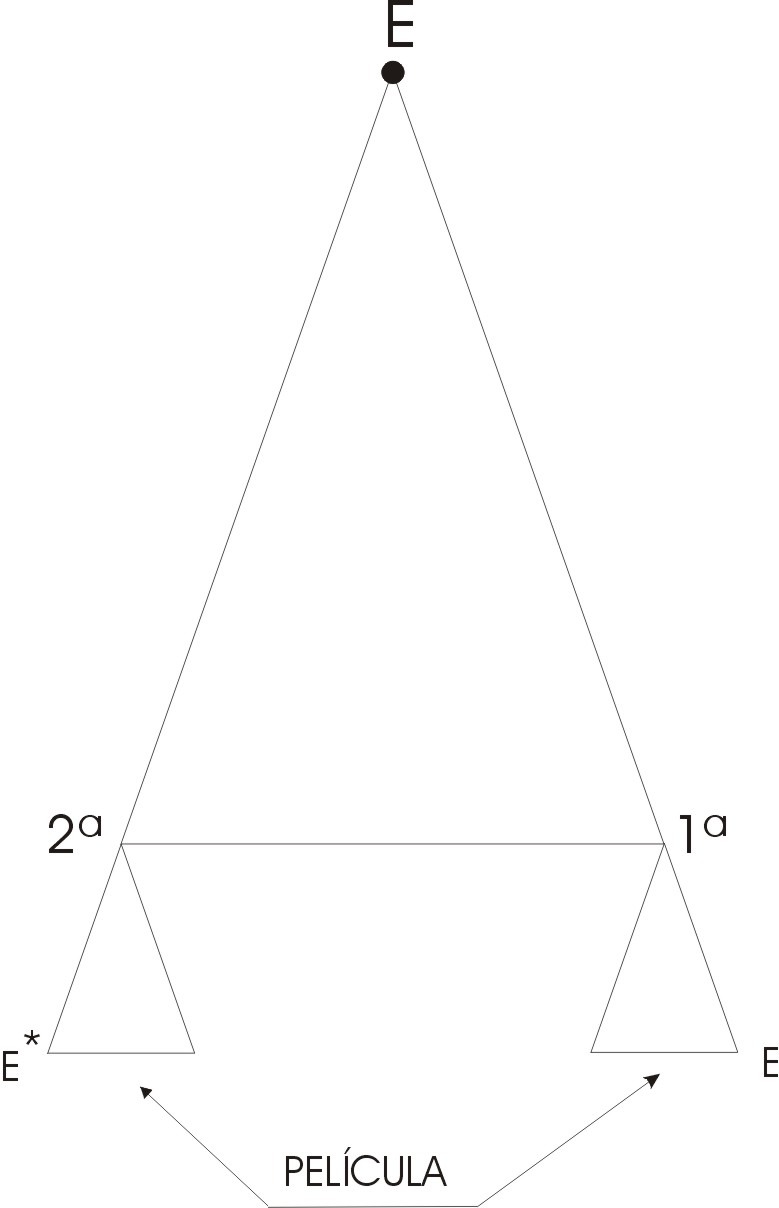 obtenidos al fotografiar la Estrella E desde las dos posiciones indicadas en la figura.

Los triángulos pequeños vienen determinados por el foco y la placa fotográfica, siendo E y E* la posición de la estrella E en la placa, al superponer los clichés (la superposición se hace utilizando de referencia un elemento fijo, en nuestro caso la máquina de escribir). Todos los triángulos son SEMEJANTES, luego podemos establecer la proporción siguiente:

distancia focal (f) es a la distancia E*E (d)

como

distancia de la estrella al Sol (D) es al diámetro de la Eclíptica ( distancia entre la posición 1ª y 2ª)(T)

Datos de partida: 

Distancia 1ª2ª = (T) diámetro de la eclíptica.

Distancia focal de la cámara (f) (específica de la cámara)

Distancia entre posiciones de la estrella en la foto (d), la composición de fotos se realiza superponiendo las estrellas fijas en un programa de tratamiento de imágenes EE* 

Cálculos:

f . T = D . d

luego D = (f . T)/d

Con el fin de que comprendas los conceptos expuestos, analiza en la escena siguiente, lo que ocurre con la posición aparente E' del punto E (proyección sobre el fondo fijo), cuando lo observamos desde distintas posiciones a lo largo del recorrido AB (estamos situados en C). Arrastra con el ratón el punto C o el E para realizar el estudio.

La cámara de fotos nos graba la posición de E' respecto de los puntos fijos Q y R, en un triángulo semejante, debido a la linealidad de los rayos de luz. Al superponer las imágenes, utilizando Q y R como elementos de referencia, podemos calcular el desplazamiento que ha experimentado E' al desplazarnos nosotros con C.

Analiza, una vez que hayas utilizado los conceptos de la escena, lo que te he señalado con las tomas fotográficas y verás como los elementos utilizados te resultan más claros.

Contesta a las preguntas siguientes:

a) ¿Qué ocurre con el ángulo de paralaje cuando la estrella está muy lejana?

b) ¿Relaciona el ángulo de paralaje con el desplazamiento de la estrella sobre el fondo fijo?

c) ¿Crees que éste método se puede aplicar en todos los casos?

d) ¿Consideras que si la estrella está muy lejana, tendremos precisión suficiente para poder calcular la distancia? ¿Qué tendríamos que hacer para mejorarla?

Notas:

1ª - Llamamos paralaje de un astro al ángulo bajo el que se vería desde este astro una longitud convencionalmente elegida, situada a distancia de la Tierra. Para los astros del sistema solar se usa el radio de la Tierra y para las estrellas el radio orbital. (Enc. Larouse) (volver)

2ª - Orbita: Es la línea imaginaria que describe un planeta alrededor de su estrella. (volver)

3ª- Astro: Cuerpo celeste, en general; como las estrellas, planetas, satélites, cometas y asteroides. (Enc. Encarta) (volver)

4ª - Estrella: es un astro con luz propia. (volver)

5º.- Tener presente que la distancia AA' es el diámetro de la órbita terrestre. (volver) 

6º.- Es necesario tener presente, en este caso, que las distancias estelares son mucho mayores que las que se observan en el ejemplo del segundo applet. Está preparado para comprobar el fenómeno, no para utilizarlo para el cálculo de distancias estelares. (volver)

autor: Pedro González Justo (miembro del grupo de astronomía CYGNUS)