

En toda esta página consideraremos dos funciones f(x) y g(x) con límite infinito o menos infinito en un cierto punto a.
Es decir
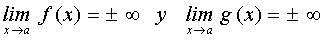
|
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite cuando x tiende al punto a de f(x)/g(x) es más infinito. |
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite cuando x tiende al punto a de f(x)/g(x) es menos infinito. |
|
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite cuando x tiende al punto a de f(x)/g(x) es más infinito por la izquierda y menos infinito por la derecha. |
El parámetro t que aparece en esta gráfica permite que trabajemos con distintas funciones f(x). Todas ellas tienen límite infinito en el punto a, pero el cociente entre f(x) y g(x) va cambiando. Selecciona un valor cualquiera para t, tanto positivo como negativo. Después, acerca la x al punto a para averiguar cuánto vale el límite del cociente cuando x tiende al punto a. Repite el ejercicio para distintos valores de t y observa que se puede obtener cualquier límite. |
|
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite de f(x)/g(x) cuando x tiende al punto a es uno. |
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite de f(x)/g(x) cuando x tiende al punto a es cero. |
Infinitos.
Se dice que una función, f(x), es un infinito en un punto a si
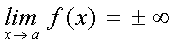
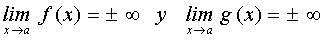
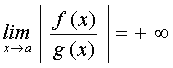
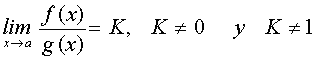

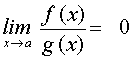
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||