siendo a, b y c números reales cualesquiera con a distinto de cero. (Observa que si a=0 se trataría de la función lineal y=bx+c).

Cuando una función es de este tipo se dice que la y depende cuadráticamente de la x. La gráfica de este tipo de funciones es una curva denominada parábola. Sin más que variar a , b y c en la imagen adjunta, obtendrás distintas funciones cuadráticas. Contesta a las preguntas que se te plantean al margen referentes a sus propiedades.

	Modifica los valores de a, b y c e intenta encontrar un significado gráfico para cada uno de ellos. ¿Qué aspectos de la gráfica se modifican al modificar alguno de esos tres parámetros?
	Determina el dominio y el recorrido de cualquier función cuadrática en función de los valores de los tres parámetros.
	Estudia sus intervalos de monotonía y sus extremos relativos. ¿Qué pasa si a es negativo?
	Estudia sus posibles simetrías. ¿Son funciones pares, impares o ninguna de ambas cosas?
	¿Son funciones acotadas? Si la respuesta es afirmativa, ¿superior, inferiormente o ambas cosas a la vez? Determina sus extremos absolutos (si los tiene).

Al igual que en el caso anterior veamos una aplicación práctica. Se trata de un problema económico:

Tenemos que cercar una finca rectangular que linda con una carretera. La valla que queremos poner del lado de la carretera cuesta a 24 euros/metro y la que queremos poner en los otros tres lados cuesta a 12 euros/metro. Se trata de averiguar qué dimensiones debe tener la finca para que su área sea máxima, sabiendo que tenemos un presupuesto de 4320 euros.

Veamos primero el planteamiento del problema. Si llamamos x al lado de la finca que linda con la carretera e y al otro lado, se trata de hallar el valor máximo de la función Área=xy. Se trata de una función de dos variables que no hemos estudiado, pero el problema nos da algunos datos que nos permiten encontrar una relación entre x e y, esa relación es la siguiente:

de donde despejando tenemos

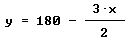
y, por tanto, el área viene representada por la función cuadrática

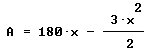
La gráfica de la izquierda es una simulación de las posibilidades del problema, suponiendo que el eje X es la carretera. La gráfica de la derecha muestra la gráfica de la función área y nuestro objetivo es hallar el valor de x para el que esa función tiene un máximo. Es decir, debemos hallar el máximo absoluto de esta función (que en este caso será también relativo). Este problema se puede resolver mediante otras técnicas de cálculo que verás en otro tema, pero el planteamiento que se hace aquí es probablemente mucho más intuitivo.