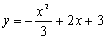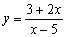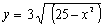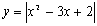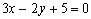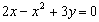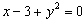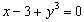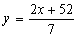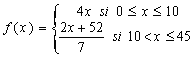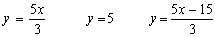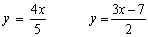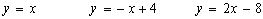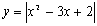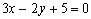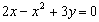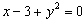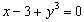En los capítulos precedentes hemos visto cómo las funciones, sean del tipo que sean, suelen admitir una expresión del tipo y = f(x). Hemos visto también que es especialmente interesante (pues facilita la obtención de información) que la expresión f(x) sea de tipo matemático. Hasta ahora hemos trabajado con expresiones simples como por ejemplo:
Sin embargo, con mucha frecuencia, las expresiones analíticas que aparecen en las Ciencias Sociales no admiten una única formulación para todos los valores de la variable independiente, de manera que es necesario utilizar diferentes fórmulas para la función según los distintos valores de x. De este tipo de funciones se dice que están definidas a trozos.
Por otra parte en las funciones del tipo y=f(x), la relación entre ambas variables x e y está claramente determinada. Por ese motivo la expresión y=f(x) recibe el nombre de forma explícita de la función. Sin embargo, en algunas ocasiones la relación entre las variables de la función no viene expresada de una forma tan clara sino a través de una ecuación que las liga, como por ejemplo:
Aunque más tarde analizaremos con detalle estos cuatro ejemplos, ya podemos decir que esta manera de representar una función recibe el nombre de forma implícita de la función.
Funciones definidas "a trozos".
Volvamos al primero de los ejemplos de esta unidad didáctica: las cuatro gráficas del ejemplo de las distancias y el recorrido en bicicleta. Los cuatro son casos de funciones definidas a trozos. En lo que sigue vamos a suponer que x representa el tiempo medido en minutos e y representa la distancia recorrida medida en km. Observa que las cuatro gráficas están formadas por segmentos que, aunque están conectados unos con otros, presentan una cierta "fractura" en sus conexiones. Ésa suele ser una señal inequívoca de que se trata de funciones definidas a trozos.
Realiza las actividades que se indican en cada una de las cuatro gráficas:
|
|
Usa la imagen de la izquierda para dibujar la gráfica de la función y=4x. ¿Coincide la gráfica de esta función con parte de la gráfica de la trayectoria de Paco? Si la respuesta es afirmativa, indica entre qué valores de x es eso cierto. Haz lo mismo con la gráfica de la función
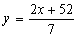
Si has contestado bien a las cuestiones anteriores y recuerdas el dominio de la función de este ejemplo obtenido en la página "Elementos" te darás cuenta de que la expresión analítica de esta función es la siguiente:
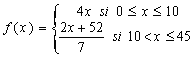
|
|
|
Usa la imagen de la izquierda (gráfica de Lidia) para dibujar las gráfica de las funciones
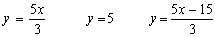
¿Coinciden las gráficas de estas funciones con alguna parte de la gráfica de la trayectoria de Lidia? Si la respuesta es afirmativa, indica entre qué valores de x es eso cierto y escribe esta función como una función definida a trozos, siguiendo el modelo del ejemplo anterior.
|
|
|
Usa la imagen de la izquierda (gráfica de María) para dibujar las gráfica de las funciones
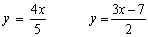
¿Coinciden las gráficas de estas funciones con alguna parte de la gráfica de la trayectoria de María? Si la respuesta es afirmativa, indica entre qué valores de x es eso cierto y escribe esta función como una función definida a trozos, siguiendo el modelo del ejemplo anterior.
|
|
|
Usa la imagen de la izquierda (gráfica de Yolanda) para dibujar las gráfica de las funciones
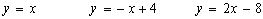
¿Coinciden las gráficas de estas funciones con alguna parte de la gráfica de la trayectoria de Yolanda? Si la respuesta es afirmativa, indica entre qué valores de x es eso cierto y escribe esta función como una función definida a trozos, siguiendo el modelo del ejemplo anterior.
|
Veamos ahora algunas funciones matemáticas muy sencillas que pueden ser expresadas como funciones definidas a trozos. Dibuja las funciones que se te indican al margen y después escríbelas en el cuaderno como funciones definidas a trozos. Si no sabes cuál es la sintaxis correcta para escribir esas funciones pulsa en el botón de ayuda.
|
| y = |x| |
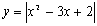 |
| y = Ent(x) |
| y = sgn(x) |
Funciones expresadas en forma implícita.
Como dijimos al principio una función puede venir expresada en forma explícita o implícita. Todas las funciones del apartado anterior eran explícitas, pues la relación entre las variables x e y estaba expresada con total claridad. Sin embargo, en los ejemplos del principio
la relación entre ambas variables viene dada por una ecuación en la que hay que despejar la variable dependiente para poder encontrar la relación entre ambas. Cuando nos encontramos con una expresión implícita hay que tener un poco de cuidado, pues no vale cualquiera. De hecho, una de las anteriores expresiones no corresponde a una función. ¿Sabrías decir cuál es y por qué? Dibujar las cuatro expresiones anteriores puede servirnos de ayuda. Hazlo usando la gráfica anterior.