
ASÍNTOTAS |
Las ramas infinitas de una función se dan cuando la x, o la y=f(x), o ambas tienden a infinito.
Cuando la curva se acerca a una recta cuando x o y tienden a infinito, dicha recta se llama ASÍNTOTA de la gráfica, cuando no se acerca a ninguna recta se llama RAMA PARABÓLICA.
| Si |
ASÍNTOTA VERTICAL |
| Si |
ASÍNTOTA HORIZONTAL |
En esta escena está representada la función 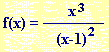 y su asíntota vertical x=a. y su asíntota vertical x=a. También está representada otra recta vertical x=k. Le puedes dar al parámetro k el valor adecuado para que la recta x=k coincida con la asíntota vertical de la curva, x=a. O bien puedes introducir directamente el valor de k en la ecuación x=k y pulsar ENTER. De esta forma se superpondrá la recta verde sobre la azul, que es la asíntota correcta. ¿Cuál es el límite de la función cuándo |
Con este ejemplo habrás observado que la asíntota vertical tiene de ecuación x=1
Justamente el .
Por tanto para averiguar las asíntotas verticales de una función, basta igualar a cero el denominador. Las soluciones de la ecuación resultante serán asíntotas verticales, si no se anula también el numerador.
Averigua las ecuaciones de las asíntotas verticales de las siguientes funciones, ayudándote de la escena adjunta.
| a) b) c) ¿Cuál es el límite de cada una de estas funciones cuando x® a por la izquierda y por la derecha? De nuevo te puedes ayudar de la escena dando a la abcisa de P, P.x valores cada vez más próximos a a, por la izquierda o por la derecha. |
Aquí tenemos representada la función ![]() y su asíntota horizontal y = b
y su asíntota horizontal y = b
También está representada otra recta vertical y=k.
Le puedes dar al parámetro k el valor adecuado para que la recta y=k coincida con la asíntota horizontal de la curva, y=b. O bien puedes introducir directamente el valor de k en la ecuación y=k y pulsar ENTER. De esta forma se superpondrá la recta verde sobre la azul que es la asíntota correcta.
¿Cuál es el límite de la función cuándo x® ¥ y cuándo x® -¥? Para averiguarlo puedes ayudarte de la escena moviendo el punto P, cambiando su abcisa P.x a valores cada vez mayores, positivos o negativos.
Con este ejemplo habrás observado que la asíntota horizontal tiene de ecuación y=2
Por tanto para averiguar las asíntotas horizontales de una función, basta hallar el límite de la función cuando x® ¥ y cuando x® -¥. Si el primer límite es un número finito b, la recta y=b es asíntota horizontal en la parte derecha de la curva, si el segundo límite es un número finito b, la recta y=b es asíntota horizontal en la parte izquierda de la curva. Si ocurren las dos cosas, simplemente se dice que y=b es una asíntota horizontal de la curva.
Averigua las ecuaciones de las asíntotas horizontales de las siguientes funciones, ayudándote de la escena adjunta.
a) |
b) |
c) |
¿A qué tiende cada una de estas funciones cuando x® ¥ y cuando x® -¥ ?
De nuevo te puedes ayudar de la escena dando a la abcisa de P, P.x, valores cada vez mayores positivos (¥), o cada vez mayores en valor absoluto negativos (-¥).
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||