| Dominio
Lo
primero que hay que estudiar en una función es su dominio, o conjunto
de valores x para los cuales f(x) existe o está definida: Df=
{xÎR: $
y=f(x)}
Hay funciones que se crean
artificialmente dando por definición el dominio (funciones definidas a
trozos) o bien se tratan de funciones que modelizan una situación real que no tiene sentido para ciertos valores de x aunque
matemáticamente se pueda calcular.
Las funciones polinómicas están
definidas en todo R.
Las funciones racionales
(cociente de polinomios), no están definidas en los valores que anulan
el denominador.
Ejemplo:
y=(3x2-5x-6)/(x2-x-2)
no está definida ni para x=-1 ni para x=2. Es decir Df=R -
{-1,2}
Las funciones irracionales (con
radicales) y= g(x)m/n están definidas en todo R si el índice
n es impar y sólo para los valores de x que hacen el radicando mayor o
igual que cero si el índice n es par.
Ejemplo:
El dominio de y=x3/2
es D={xÎR: x>=0}.
El dominio de y=(x2-x-2)1/2
es D=R-(-1,2); no está definida para x2-x-2<0 es decir en
el intervalo abierto de extremos -1 y 2.
La función logarítmica y= logax
está definidas para x>0. En general y=loga g(x)
esta definida para los x tales que g(x)>0.
Ejemplo:
y=ln (x2-4)
no está definida en x tal que x2-4<0, es decir en
abs(x)<2 que representa el intervalo (-2,2); por tanto el dominio es
D=R-(-2,2)
Las funciones y=sen(x), y=cos(x)
e y=ax están definidas para todo x.
La función trigonométrica
y=tg(x) no está definida para x=p/2+kp,
kÎZ
La función definida como:
y=ex-1 para x>=0
tiene un dominio artificial y por alguna conveniencia o por ser modelo
de algún fenómeno real no tiene interés considerar x<0.
La función siguiente está
definida a trozos:
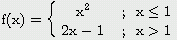
el dominio es R pero este está
dividido en dos intervalos; estando cada intervalo regido por una
expresión distinta
Continuidad
Las funciones
conocidas (salvo
las definidas artificialmente) son continuas donde están definidas.
Derivabilidad
También son derivables en el
dominio de definición las funciones habituales. Aparecen puntos
angulosos cuando se utiliza la función valor absoluto y en algunos
radicales en el punto donde el radicando es cero.
Ejemplo:
y=abs(x-1), está
definida y es continua en R pero no es derivable en x=1 (punto
anguloso)
Ejemplo:
y=x2/3
está definida y es continua en R pero presenta un punto anguloso en
x=0.
| Funciones permitidas
por Descartes
Las funciones que no se
escriben como habitualmente hacemos sobre el papel son:
Raíz cuadrada:
sqrt(x)
Logaritmo neperiano:
log(x)
No confundir esta
notación con la del logaritmo en base 10.
Logaritmo en
base a, (logax): log(x)/log(a)
Tangente
trigonométrica tg(x): tan(x)
Arco tangente, arc
tg(x): atan(x) |
|
