
La Hipérbola
La hipérbola es el lugar geométrico de los puntos tales que la diferencia de sus distancias a dos puntos fijos, llamados focos, es constante. En la siguiente escena mide las distancias de varios puntos de la hipérbola a los focos F y G y comprueba que la diferencia de estas distancias siempre es constante.
En una hipérbola hay que destacar los siguientes elementos:
El eje Focal que es la recta que pasa por los focos, eje secundario a la mediatriz del segmento que determinan los focos.
Los focos F y G y la distancia focal que se representa por 2c.
Los vértices A y A´ que son los puntos intersección de la hipérbola con el eje focal, el segmento AA´ cuya longitud se representa por 2a.
Sean F(-c,0) y G(c,0) los focos de una hipérbola y sea 2a la diferencia de las distancias de los puntos de la hipérbola a los focos. La siguiente escena muestra un punto P que cumple la propiedad:
PF - PG = 2a
Ejercicios:
1) Arrastra el punto P y
verás que el rastro que deja es una hipérbola.
2) Cambia el valor de a entre -2.5 y 2.5 y dibuja las hipérbolas
correspondientes.
¿Qué ocurre cuando a=0?
¿Qué ocurre cuando al cambiar a por -a?
3) Demuestra que la formula de la hipérbola centrada en
el origen es 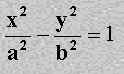
En la escena siguiente da valores a a y b
Ejercicios:
1) ¿Qué ocurre cuando a y b son iguales?.
2) ¿Qué ocurre cuando b es mayor que a?
Veamos que ocurre con la excentricidad en las hipérbolas en la siguiente escena.
Ejercicios:
1) Da varios valores a a y c y comprueba que ocurre con la
excentricidad. Entre que valores esta la excentricidad en la hipérbola.
2)¿qué ocurre con la hipérbola cuando la excentricidad se aproxima a
uno?
3) ¿Qué ocurre cuando e se hace cada vez más grande?
Asintotas
Se llama asíntota de una hipérbola a la recta que pasa por el centro de la misma y es tangente a la hipérbola en el infinito.
En la siguiente escena da valores a m1 y m2 hasta que creas que son las asintotas, cambia varias veces los valores de a y b y repite el ejercicio.
1) ¿Cual crees que es la ecuación de las asintotas?
La ecuación de las asintotas son y = ±(b/a)x.
Si a y b son iguales entonces estamos ante una hipérbola equilátera.
Autor: Antonio Caro Merchante
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||