
VECTORES |
a) Cualquier vector v se puede poner como combinación lineal (C.L.) de otros dos x e y de distinta dirección.
|
|
b) Esta C.L. es ÚNICA. Es decir, dados x, y y v, sólo existen un par de números a y b que cumplen la igualdad anterior.
c) Observa también que los propios vectores x e y se pueden poner como C.L. de ellos mismos:
|
|
|
e) Si los vectores de la base son perpendiculares entre sí, se dice que forman una base ortogonal y si, además, tienen módulo 1, se dice que forman una base ortonormal.
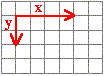 |
Base ORTOGONAL |
|
 |
Base ORTONORMAL |
|
| En esta escena tenemos la base ortogonal B(x,y)
y el vector z,
que en principio tiene de coordenadas (2,3)
respecto de dicha base, ya que
Cambiando los valores de a y b puedes ver las distintas coordenadas que va teniendo los distintos vectores z y la C.L. de x e y que nos da z, pues |
Halla las coordenadas del vector x respecto de la base B(u,v)
| 1.- Hay que formar un paralelogramo con las
prolongaciones de los vectores u
y v (Variando
a y b),
de tal forma que x
sea una diagonal del mismo.
Por tanto esta vez, te conviene prolongar u en el sentido opuesto, o sea en el de -u, y v en su mismo sentido. 2.- A continuación tienes que trazar paralelas a u y v desde el extremo de x, A, para completar el paralelogramo. 3.- Escribe en tu cuaderno x como C.L. de u y v |
|
| 4.- Escribe las coordenadas de x respecto de la base B(u,v) | |
|
Mueve con el ratón los extremos de u y/o v para comprobar la suma para otras coordenadas. Por ejemplo si u=(-4,0) y
¿Cuáles son las coordenadas de u+v? |
| Cambiando los valores de a y b, dibuja el
vector
1.5u + 2v En este caso tenemos:
Este resultado lo puedes ver en la escena, si haces a=1.5 y b=2 ¡Fíjate bien en el dibujo de los vectores para comprobar sus coordenadas! |
|
|
EJERCICIO 12 1.- Calcula en tu cuaderno las coordenadas, respecto de la base B(x,y), de los vectores: 2.- Compruébalo después cambiando a y b, según convenga, en la escena anterior. 3.- Puedes hallar otras combinaciones lineales que tu quieras y comprobar los resultados en la escena. |
|
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||