
VARIABLES ESTADÍSTICAS BIDIMENSIONALES.
REGRESIÓN Y CORRELACIÓN (1)
Variables estadísticas bidimensionales
Tipos de dependencia a partir de la representación gráfica
Covarianza y su interpretación
Variables estadísticas bidimensionales
Se trata de variables que surgen cuando se estudian dos características asociadas a la observación de un fenómeno.
Ejemplo 1.- Estudiamos la talla, medida en cm. y el peso, medido en kg. de un grupo de 10 personas, podemos obtener los siguientes valores:
| TALLA (cm) | 160 | 165 | 168 | 170 | 171 | 175 | 175 | 180 | 180 | 182 |
| PESO (kg) | 55 | 58 | 58 | 61 | 67 | 62 | 66 | 74 | 79 | 83 |
Podemos llamar X a la talla e Y al peso con lo que se obtendría la variable bidimensional (X, Y) que toma 10 valores, que son las 10 parejas de valores de la tabla anterior: (160,55), (165,58), etc.
Cuando el número de valores de la variable bidimensional no es muy grande, los mismos se expresan en una tabla semejante a la anterior, pero en algunos casos el número de "parejas" de valores (x,y) es grande y además muchos de ellos aparecen repetidos; en este caso se utiliza una "Tabla de doble entrada" como la que se muestra a continuación en el ejemplo 2.
En la primera fila se colocan los valores de una de las características o variable que componen la variable bidimensional y en la primera columna los de la otra.
Ejemplo 2.- Se representa por X el número de hijos de 100 familias y por Y el número de hijas:
nº hijas (Y) |
0 |
1 |
2 |
3 |
|
nº hijos (X) |
----------- |
-- |
-- |
-- |
-- |
0 |
----------- |
10 |
15 |
15 |
3 |
1 |
---------- |
10 |
12 |
7 |
2 |
2 |
---------- |
8 |
4 |
3 |
1 |
3 |
---------- |
3 |
2 |
1 |
0 |
4 |
---------- |
2 |
1 |
1 |
0 |
La lectura de esta tabla es sencilla. Por ejemplo: habría 7 familias que tendrían 1 hijo y 2 hijas y ninguna familia tendría 3 hijos y 3 hijas.
En realidad la tabla de doble entrada anterior se convertiría en una tabla simple si escribiéramos los 100 pares de valores iguales o repetidos en una tabla simple.
Los ejemplos con que vamos a trabajar este tema serán del primer tipo por razones de limitación a la hora de visualizar más número de valores en las escenas. Esto no limita las posibilidades de estudiar el tema y entender los conceptos básicos.
Representación gráfica: Diagramas de dispersión o nubes de puntos
La representación gráfica de este tipo de variables es en realidad semejante a la respresentación de puntos en el plano, usando unos ejes de coordenadas. Cada pareja de valores da lugar a un punto en el plano y el conjunto de puntos que se obtiene se denomina "diagrama de dispersión o nube de puntos".
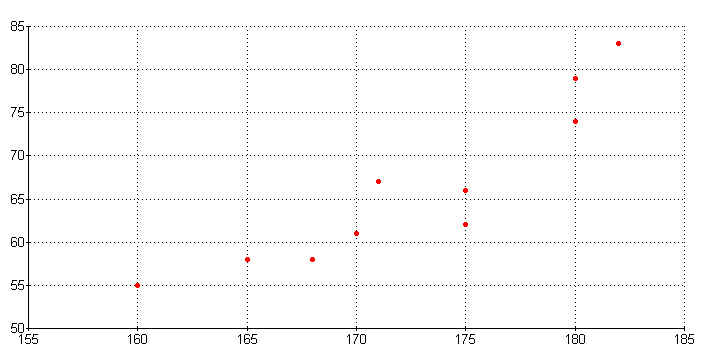
En el ejemplo 1 anterior en el que se estudiaba la talla y el peso de 10 personas se obtendría el siguiente diagrama de dispersión: (En el eje X se representa la talla en cm. y en el eje Y el peso en kg.)
En la escena siguiente se puede observar otro diagrama de dispersión correspondiente a una variable bidimensional que toma 6 valores a los que hemos llamado:
(a , a1), (b , b1), (c , c1), (d , d1), (e , e1), (f , f1)
Si se van cambiando usando las ventanitas inferiores de la escena, los valores de la variable, se pueden observar los cambios en la nube de puntos.
Tipos de dependencia a partir de la representación gráfica
Uno de los objetivos de este tema es estudiar el tipo de dependencia que hay entre las dos características o variables estudiadas para que fenómeno en cuestión. Por ejemplo:
" ¿ A mayor talla de una persona le correspode mayor peso ? "
" ¿ Cuanto mayor es el número de hijos varones de una familia mayor es el número de hijas ? "
A estas cuestiones parece que se responde rápidamente que sí. Pero
¿Cómo se observa en la nube de puntos este hecho?
Se puede ver en el primera figura que correspondía al diagrama de talla - peso que la serie de puntos presenta una tendencia "ascendente" . Se dice en este caso que existen entre las dos variables una "dependencia directa" .
En caso en que la tendencia sea "descendente" se diría que estaríamos ante una " dependencia inversa "
Naturalmente en caso en que no se pueda observar una tendencia clara estaríamos ante una dependencia muy débil que no se puede observar mediante la nube de puntos y se verá cómo estudiarla a continuación.
Ejercicio 1
- En la escena que correspondía a la variable con 6 pares de valores: ¿Qué se puede decir de la dependencia para los valores que aparecen inicialmente?
- Modifica dichos valores para que la dependencia sea directa y posteriormente inversa.
Covarianza y su interpretación
Una medida específica de las variables bidimensionales es la covarianza.
Para variables expresadas mediante una tabla simple (sin pares de valores repetidos), la covarianza se calcula mediante la formula:
![]()
Donde xi
e yi
representan los pares de valores de la variable y el producto ![]() corresponde al producto de las medias aritméticas de las
variables x e y respectivamente.
corresponde al producto de las medias aritméticas de las
variables x e y respectivamente.
Calculemos la covarianza para el ejemplo primero correspondiente a la variable talla - peso:
La suma de todos los productos de los valores de x (talla) por los de y (peso) sería:
160 · 55 + 165 · 58 + 168 · 58 + 170 · 61 + 171 · 67 + 175 · 62 + 175 · 66 + 180 · 74 + 180 · 79 + 182 · 83 = 114987 que dividido por el número de valores (10) será: 11498,7
A este valor debemos restarle el producto de las medias de ambas variables que naturalmente sabes calcular:
Media de x (talla): 172,6
Media de y (peso): 66,3
Con lo que la covarianza Sxy = 11498,7 - 172,6 · 66,3 = 55,32
(Con una calculadora con funciones estadísticas este cálculo es sencillo).
Hemos obtenido un valor positivo para la covarianza que corresponde a una dependencia directa como ya habíamos intuido con la nube de puntos.
En el ejemplo 2 (hijos - hijas) se puede comprobar que también la covarianza es positiva. (Se deja como ejercicio la comprobación). Téngase en cuenta que en este caso la variable bidimensional toma "100 valores"
Ejemplo 3.- Partimos de la escena siguiente, en la que se pueden ver inicialmente la nube de puntos de la variables bidimensional que toma los siguientes 6 pares de valores:
| x | 2 | 4 | 6 | 8 | 10 | 12 |
| y | 8 | 7 | 7 | 6 | 6 | 4 |
Ejercicio 2
- A la vista de la nube de puntos ¿qué tipo de dependencia se puede suponer?
- Calcular la covarianza y confirmar la afirmación anterior
Efectivamente habrás obtenido una covarianza negativa (-3,5) y por tanto la dependencia se inversa.
Ejercicio 3
- Calcular la covarianza de la variable hijos-hijas del ejemplo 2 y deducir del valor el tipo de dependencia.
Autor: Leoncio Santos Cuervo
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||