
SISTEMAS DE ECUACIONES
Sistemas lineales de primer grado con dos incógnitas :
......................................Resolución gráfica
..........................................Resolución numérica
Dos casos especiales: Ecuaciones que no tienen solución
...................................Ecuaciones con infinitas soluciones
Sistemas de ecuaciones de grado superior
Llamamos sistema de ecuaciones a un conjunto cualquiera de ecuaciones . Por ejemplo las ecuaciones:
3x2 - 2x + 3y = y - 1
2y - 3y2 = 3x + 4
Formarían un sistema de dos ecuaciones con dos incógnitas
x + y + z = 4
El conjunto de ecuaciones: ......................................... 3x - 2y - z = 4
....x + 3y - 5z = -1
Formarían un sistema de tres ecuaciones con tres incógnitas.
Se llama grado del sistema de ecuaciones al mayor exponente al que se encuentre elevada alguna incógnita del sistema.
El ejemplo anterior es un sistema de dos ecuaciones con dos incógnitas de segundo grado.
El sistema de ecuaciones ![]() es de primer grado con dos incógnitas.
es de primer grado con dos incógnitas.
Cuando el sistema de ecuaciones es de primer grado y además no aparecen términos con las incógnitas multiplicadas entre sí (tipo x.y) se dice que es un sistema de ecuaciones lineales.
Es con este tipo de sistemas y para el caso de dos incógnitas, con los que vamos a trabajar esencialmente en este tema.
SISTEMAS DE ECUACIONES LINEALES, DE PRIMER GRADO, CON DOS INCÓGNITAS
Ejercicio 1.-
Supongamos que queremos resolver el sistema de ecuaciones: ![]()
Si damos valores a una de las dos incógnitas y obtenemos los correspondientes a la otra, en cada ecuación del sistema, de cada ecuación obtenermos un conjunto de puntos (x , y), que representados en los eje de coordenadas, dan lugar a una recta.
En este caso, obtenemos:
Para la primera ecuación 2x + y = 0, los puntos (0 , 0) ; (1 , -2), suficientes para representar la recta.
Para la segunda ecuación x + y = -1, los puntos (0 , -1) , (3 , -4) para representar la segunda.
Obsérvese la escena siguiente que representa ambas rectas.
Observa las ecuaciones del sistema anterior también en la pantalla. Mueve al punto rojo con el ratón hasta conseguir que la pirmera valga 0 y la segunda -1.
¿Cuál es el punto en el que se encuentra la solución?
¿Cuánto valen la x y la y en ese punto? Sustituye dicho valor de x e y en las ecuaciones y comprueba que efectivamente se cumplen.
En la escena siguiente se puede apreciar con detalle dicha solución:
Como puede verse las dos rectas se cortan en el punto de coordenadas (1,-2).
" Eso quiere decir que la solución del sistema es x = 1, y = -2."
Efectivamente, si en las ecuaciones del sistema sustituimos x por 1 e y por -2 se obtiene:
2·1-2 = 0; 2-2 = 0, "cierto" para la primera
1-2 = -1, "cierto" para la segunda.
Lo que acabamos de hacer es resolver gráficamente el sistema de ecuaciones.
Ejercicio 2.-
Resolver gráficamente el sistema de ecuaciones: 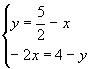
Utiliza la escena siguiente para cambiar las ecuaciones en las ventanas correspondientes de colores rojo (ya está escrita correctamente) y azul (puedes cambiarla por la expresión original).
Atención con la forma de escribir las expresiones: producto * (no olvides que 2x es 2*x) y cociente /.
Para encontrar la solución, cambia los valores de x e y hasta que las rectas verdes se corten en el punto solución.
Habrás observado que la solución es: x = 0,5 (-3/2) e y = 3.
Para resolver cualquier otro sistema de ecuaciones basta con que cambies las ecuaciones en las ventanas inferiores de esta pantalla.
Quizás ya hayas trabajado en clase resolviendo
sistemas de ecuaciones y que existen varios métodos para ello.
Por ejemplo el primer sistema que resolvimos en el ejercicio 1: ![]()
Se resuelve fácilmente por cualquiera de ellos:
Por sustitución:
- 1 - Se despeja una incógnita en una ecuación, por ejemplo la y en la primera: y = -2x
- 2 - Se sustituye dicho valor en la segunda: x - 2x = -1
- 3 - Se resuelve esta ecuación: -x = -1 ; x = 1
- 4 - Con este valor se halla el de la otra incógnita (paso 1): y = -2
Solución que naturalmente coincide con la obtenida antes gráficamente.
Por reducción:
-1 - Se consigue que en al sumar o restar ambas ecuaciones, miembro a miembro se elimine una incónita. Para ello se simplifica todo lo posible y se multiplica, si es necesario alguna ecuación por algún número. En este caso se pueden restar directamente una ecuación de la otra y se elimina la y : 1ª - 2ª : x = 1
- 2 - Se resuelve la ecuación resultante. En este caso ya lo está ya que hemos obtenido directamente la solución para la x:
x = 1
- 3 - Se sustituye esta solución en una de las dos ecuaciones y se resuelve hallando la otra incógnita. En este caso, sustituyendo x = 1 en cualquiera de las dos ecuacioens se obtiene fácilmente y = -2.
( Dejamos sin comentar aquí el tercero de los métodos más conocidos "igualación", por considerar suficientes los dos métodos citados ).
Ejercicio 3.- Resuelve numéricamente en tu cuaderno de trabajo el sistema del ejercicio 2. Elige el método que creas más adecuado y comprueba que la solución coincide con la obtenida antes gráficamente.
Elige de tu libro sistemas de ecuaciones, resuélvelos numéricamente por alguno de los dos métodos citados y comprueba gráficamente la solución escribiendo las ecuaciones en la escena del apartado anterior correspondiente a la resolución gráfica.
SISTEMAS DE ECUACIONES QUE NO TIENEN SOLUCIÓN
Ejercicio 3.-
Resuelve en el cuaderno de trabajo el siguiente sistema de
ecuaciones: ![]() .
.
Seguramente habrás llegado a una expresión como 0 = -8 o algo parecido. ¿Qué significa?. Desde luego eso no es cierto.
Observa la siguiente escena::
¡Las dos rectas son paralelas!, luego no hay punto de corte. Eso significa que el sistema de ecuaciones:
no tiene solución.
SISTEMAS DE ECUACIONES CON INFINITAS SOLUCIONES
Ejercicio 4.- Resuelve
en el cuaderno de trabajo el siguiente sistema de ecuaciones: ![]()
Ahora habrás llegado a la expresión 0 = 0 u otro número = el mismo número.
¿qué significa ahora?.
La igualdad que has obtenido es cierta pero se te han eliminado la x y la y.
¿Cuál es la solución?.
Si la igualdad es cierta seguro ¿lo será para cualquier valor de x o de y?.
Observa la escena:
¡Las dos ecuaciones corresponden a la misma recta!, luego las dos rectas son la misma y por tanto tienen todos los puntos comunes. En este caso cualquier punto de la recta es solución del sistema y se dice que el sistema tiene:
infinitas soluciones (los infinitos puntos de la recta)
¿cómo hallar las soluciones?:
Señala en las flechitas inferiores cambiando el valor de x. Se moverá el punto destacado a lo largo de la recta y todos los valores que observas para x e y son soluciones
(Si se desea un valor concreto para x, basta borrar el de la ventanita inferior y cambiarlo por el deseado).
También puedes "arrastrar" el punto S, observarás que se mueve sobre la recta e irás viendo todas las soluciones.
Numéricamente se hallan dando valores a x o y en cualquiera de las dos ecuaciones (son las dos la misma) y obteniendo los correspondientes de la otra incógnita. Por ejemplo en la primera ecuación:
x - 3 = y + 1, podemos obtener para y = 0, x = 4; para y = 2, x = 6; para y = -3, x = 1; etc, todas ellas soluciones.
Muchos problemas que se resuelven mediante ecuaciones pueden necesitar más de una incógnita y dar lugar por tanto a un sistema de ecuaciones. Por ejemplo:
Problema: Encuentra dos números sabiendo que la mitad de su suma es 5 y el doble de su diferencia es 8.
Planteamiento: Números: x e y.
Ecuaciones: (x + y) / 2 = 5 ; 2(x - y) = 8
Buscar la solución en la siguiente escena, cambiando los valores de x e y. Observar las rectas verdes hasta que se encuentren el el punto deseado.
Elige otros problemas de tu libro, plantea las ecuaciones y busca las soluciones cambiando los valores de las ecuaciones en la escena anterior.
SISTEMAS DE ECUACIONES DE GRADO SUPERIOR A UNO
Los sistemas de ecuaciones de grado superior a uno (generalmente no se suelen resolver de grado mayor que 2), se resolverán gráficamente de forma idéntica a la vista para los de primer grado y de forma numérica por los mismos métodos comentados para el caso de primer grado.
Ejercicio 5.- Resolver el sistema formado por las ecuaciones: x2 + y2 = 5 ; x - y = 1
Se observa gráficamente que los puntos de corte de ambas gráficas son (2 , 1) y (-1 , -2), de ahí las correspondientes soluciones que has debido de obtener para x e y. Puedes modificar los valores de x e y en con las flechitas inferiores para observalo mejor.
Ejercicio 6.- Resuelve en tu cuaderno de trabajo algunos sistemas de ecuaciones de segundo grado que se encuentren en tu libro y comprueba gráficamente en la imagen anterior las soluciones, cambiando las ecuaciones.
Autor: Leoncio Santos Cuervo
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||