Volver al índice

LA CAJA

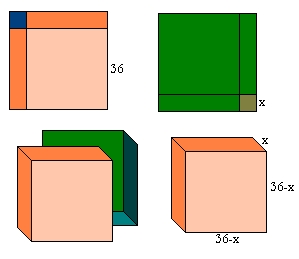Tenemos dos piezas cuadradas de 36 cm de lado. Les cortamos a cada una, una esquina cuadrada de lado x, doblamos los bordes, para unir las dos piezas y formar una caja. ¿Cuánto debe valer x, el lado del cuadradito que recortamos, para que el volumen de la caja sea máximo? La función que nos da el volumen de la caja será: V=x(36-x)2 Donde el dominio de la función será 0<x<36 ya que el cuadradito que recortamos no puede ser mayor que la pieza completa.

La forma de resolver este problema cambia por completo si lo hacemos calculando, a si lo hacemos con Descartes.

a) CON DESCARTES

Para poder ver mejor la función, hemos cambiado las unidades a dm, de tal forma que la función representada en la escena es: V=x(3.6-x)2 Y por tanto su dominio es 0<x<3.6 El parámetro a, representa los distintos valores que podemos dar a x. El parámetro función sólo toma dos valores, 0 y 1. Si vale 0 veremos la función Volumen, y si vale 1 veremos la función derivada. El punto amarillo estará sobre la función Volumen si el parámetro función=0, y estará sobre la función derivada si función=1. Averigua en esta escena cuál es el valor de x que hace máxima la función Volumen en el intervalo (0,3.6), y cuál es este valor máximo.

b) SIN DESCARTES
Hay que averiguar el máximo absoluto de la función V=x(3.6-x)² en el intervalo (0,3.6)
El máximo absoluto de una función contínua, está en el máximo relativo (f '(a)=0) o en los extremos del intervalo.
Hallamos la función derivada, averiguamos los valores de x que la hacen cero, que son x=1.2, y x=3.6 (éste no nos vale puesto que 0<x<3.6).
Ahora calculamos el valor de la función en x=1.2 y en los extremos del intervalo:
f(0)=0, f(1.2)=6.91, f(3.6)=0
Por tanto el máximo de la función se obtiene para x=1.2, f(1.2)=1.2*2.4²=6.91
¿Era lo mismo que habíamos obtenido en la escena?

---

TRIÁNGULOS RECTÁNGULOS

De todos los triángulos rectángulos cuyos catetos suman 10cm, halla las dimensiones de aquél cuya área es máxima. En esta escena tienes representado los triángulos que cumplen que la suma de sus catetos es 10. Mueve con el ratón el vértice B, y podrás obtener diferentes triángulos con las mismas condiciones. Por otra parte está representada la función área, tomando como variable el cateto x. Sin más que mover el punto B podrás buscar la solución del problema. ¿Cuál es el dominio de la función área en este problema?

Volver al índice

Anterior

Continuar

---

Autora: Ángela Núñez Castaín

	Ministerio de Educación, Cultura y Deporte. Año 2000