
| Derivadas Aplicaciones Optimización |
5.- UTILIDAD DE LA FUNCIÓN DERIVADA |
En concreto, las abcisas de los máximos y mínimos de una
función se encuentran entre las soluciones de f '(x)=0, pues en ellos la recta tangente
es horizontal, por tanto la pendiente es cero, y en consecuencia la derivada es cero
también.
Esto es, donde la función derivada corta al eje X, la función f tendrá un máximo o un
mínimo, o sea un punto de tangente horizontal.
En los ejercicios siguientes, vas a calcular la derivada de
algunas funciones, y=f(x), aplicando la fórmula: ![]() .
.
Después vas a comprobar tus resultados en las escenas correspondientes, por el siguiente
método:
También puedes ver la recta tangente en cada punto. Contesta a
las siguientes preguntas que se refieren a las tres funciones de las tres escenas
anteriores:
4.- En los puntos en que la recta tangente es horizontal, ¿cuánto vale la
derivada? ¿qué forma tiene la función? ¿dónde está la función derivada, por encima,
por debajo o en el eje X?
5.- Cuando la función es creciente, ¿qué signo tiene la derivada?
¿dónde está la función derivada, por encima, por debajo o en el eje X?
6.- Cuando la función es decreciente, ¿qué signo tiene la derivada? ¿dónde
está la función derivada, por encima, por debajo o en el eje X?
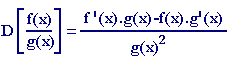
EJERCICIOS:
4.- Aplicando estas reglas, calcula ahora la derivada de las tres
funciones dadas en las escenas de más arriba de esta página. De esta forma podrás
comparar con los cálculos que hiciste, y comprobarlas en las escenas correspondientes.
5.- A continuación verás 6 escenas,
en cada una de las cuales está representada una función f(x), cuya ecuación puedes ver.
Vas a dar los siguientes pasos:
1) Calcula la derivada f '(x), de f(x), por las reglas anteriores
2) Introduce la ecuación de la derivada en la parte inferior de la escena, sustituyendo
y=f(x) por la función derivada y pulsando Enter. Se representará la función que hayas
introducido.
3) Arrastra con el ratón el punto rojo, que deberá recorrer la función que has
introducido y representado
4) Pulsa el botón función y aparecerá la expresión de la función derivada en la
escena.
6.- Apoyándote en las escenas 6 anteriores, resuelve en tu
cuaderno los siguientes ejercicios:
a) ¿Para qué valor de x la derivada vale -1 en las funciones 1ª y 2ª?
b) ¿Para qué valor de x la derivada vale 1 en las funciones 3ª y 4ª?
c) ¿Para qué valores de x la derivada vale 0 en las 6 funciones? Observa que en estos
puntos la función f(x) tiene o un máximo o un mínimo, y coincide con los puntos donde
la función derivada
f '(x) corta al eje X.
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||