ASÍNTOTAS

1.3.- Asíntotas oblícuas

Hay ramas infinitas del tipo 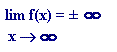asintotas2_1.gif (1199 bytes) que se ciñen a rectas de ecuación y=mx+n.

Cuando la función f(x) es el cociente de dos polinomios, y el grado del numerador supera en 1 al del denominador, entonces la curva y=f(x) tiene una asíntota oblícua cuya ecuación es y=mx+n, siendo mx+n el cociente entero de los dos polinomios.

EJEMPLO

Vamos a estudiar la asíntota oblícua de las funciones del tipo: cuyo límite cuando x®¥ es ¥ , y que por tanto tiene una asíntota oblícua

En la escena siguiente tenemos:

La gráfica de la función
La gráfica de la asíntota oblícua y=mx+n de dicha función
La regla de Ruffini para hacer la división del polinomio numerador ax²+bx+c, entre el polinomio denominador x-d
La gráfica de una recta y=2x+1, cuya ecuación se puede editar en la parte inferior de la escena, donde aparece su ecuación, o sea que puedes cambiarla y pulsar enter.

Objetivo: Averiguar la ecuación de la asíntota oblícua

En el inicio de la escena tenemos a= 1, b=-5, c=11 y d=2, o sea la función: asintotas2_3.gif (1102 bytes)

Al hacer la división por Ruffini, vemos en la escena que nos queda x-3 de cociente y 5 de resto.

Por tanto podemos escribir que:

Evidentemente si x®¥ ® 0, por lo que la función asintotas2_3.gif (1102 bytes) estará cada vez más próxima a la recta y=x-3.

Por tanto: La ecuación de la asíntota oblícua de la función es y=x-3

En la escena puedes ver, que a medida que x®¥ , o sea cuando nos desplazamos a la zona derecha del eje X, la asíntota se va acercando a la curva.

Si cambias en la escena la ecuación y=2x+1 por y=x-3 verás que la recta verde se superpone a la roja, o sea que ahora la recta verde y=x-3 es exactamente la asíntota oblícua.

En la escena puedes hacer los siguientes cambios para estudiar otras funciones del mismo tipo:

Cambiar los valores de los parámetros a, b, c y d
Una vez hayas averiguado la ecuación de la asíntota oblícua, introducirla en la ecuación de la recta verde, pulsar enter, y esta recta verde se superpondrá con la asíntota roja, lo que confirmará la bondad del resultado.

EJERCICIO 3

Averigua las ecuaciones de las asíntotas oblícuas de las siguientes funciones, ayudándote de la escena anterior.

EJERCICIO 4

Ahora vas a averiguar la ecuación de las asíntotas de una función gráficamente.

En la escena siguiente puedes dibujar la función que quieras y dibujar su asíntota.

Calcula las ecuaciones de las asíntotas, ya sean verticales, horizontales u oblícuas, de las siguientes funciones y comprueba tus resultados en la escena anterior:

Nota: Al introducir las fórmulas de las funciones, teienes que tener en cuenta la sintaxis que hay que utilizar.

FUNCIONES	Sintaxis en la escena	FUNCIONES	Sintaxis en la escena
	y=(x^2-3*x+2)/(x^2+1)		y=(x2-2*x+2)/(x-1)
	y=x^3/(x^2+1)		y=x^3/(x-1)^2
	y=(3*x-1)/(x+2)		y=x^2/(x^2-1)
	y=3*x^2/(25-x^2)		y=x^2/(x-2)

Volver al índice

Autora: Ángela Núñez Castaín


	Ministerio de Educación, Cultura y Deporte. Año 2000