
DERIVADAS II
Derivada de una función en un punto
Tangente a una curva en un punto
Como ya se ha visto la tangente en un punto de una curva se obtiene como límite de las secantes en ese punto.
![]()
1.- Comprueba cómo a medida que h tiende a cero, es decir, que el punto Q se aproxima a P, la secante QP se va aproximando cada vez más a la tengente.
Las pendientes de las secantes:
Todas las secantes pasan por el punto P (a, f(a)) y por el punto Q (a+h, f(a+h)). Por lo tanto la pendiente de las secantes será:
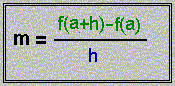
2.- Observa cómo varían las pendientes de las secantes cuando el punto Q se aproxima a al punto P.
a) Calcula la pendiente de la recta tangente en el punto de abscisa 1.
b) Calcula la pendiente en otros puntos x=2; x=2; x=0; x=-1, etc.
c) Escribe la ecuación de la recta tangente a la curva de la figura en el punto x=1.
d) Escribe la ecuación de las rectas tangente en los puntos donde las calculado las pendientes.
Definición de derivada de una función en un punto
La derivada de una función en el punto de abscisa x = a es la pendiente de la tangente a la curva, que representa esa función, en el punto (a,f(a)).
3.- Observa y anota la derivada en distintos puntos: x=1; x=2; x=0; x=-1, etc.
a) Busca dos puntos con derivada cero.
b) Busca puntos con derivada 2; 10; -2; -10; etc.
c) Observa cómo en cada caso las pendientes de las secantes QP se aproximan a la derivada.
Cálculo de la derivada de una función en un punto
Sea y = f(x) un función.
La derivada de f(x) en el punto x=a, según hemos visto, es la pendiente de la recta tangente a la curva en el punto P(a,f(a)) y se designa como f ' (a).
Hemos visto que:
![]()
Además, las pendientes de las secantes, para cada valor de h, son:
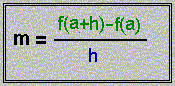
Por lo tanto, como las pendientes de las secantes se van aproximando cada vez más a la pendiente de la tangente, podemos escribir:
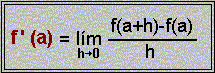
4.- Compruba nuevamente cómo los valores de m se van aproximando a la derivada cuando h tiende a cero en los siguientes puntos:
a) En x = 1.5.
b) En x = 0; x = -1; x = -2; etc.
Utiliza el cambio de escala y el desplazamiento de ejes cuando necesites ver las gráficas con más detalle.
Autor: Juan Madrigal Muga
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||