La escena siguiente muestra que el área encerrada en un recinto plano es igual número de cuadrados de lado unidad que es posible introducir en dicha figura, tal como se acostumbra a definir en Geometría elemental.
Sin embargo las cosas no son siempre tan sencillas, basta pensar en el
círculo de radio unidad, cuya área viene dada por p que
es un número irracional. Aunque consideremos el círculo de radio 
, cuya área es 1, no parece
razonable dividir el cuadrado unidad en "trozos" de manera que encajen
perfectamente en dicho círculo.
Para solucionar el problema se sigue un método de aproximaciones. Dada una función y = f (x), si se quiere hallar el área del recinto limitado por la función, el eje de abcisas y las rectas de ecuaciones y = a e y = b, se divide el intervalo [a,b] en un número de subintervalos formando con ellos como base y altura la de la función en el extremo inferior (aproximación por defecto) o superior (aproximación por exceso) sendos rectángulos, la suma de todos estos rectángulos dará la correspondiente aproximación al área buscada.
Lo dicho se muestra en las siguientes escenas
(Si quieres puedes ver la solución)
De esta forma se consigue acotar, inferior y superiormente, el área:
Sea una función y = f (x) continua en un intervalo [a,b], tendrá un máximo y un mínimo en cada uno de los subintervalos en que lo dividamos. Consideremos el intervalo i-ésimo [xi-1,xi] y sea mi el mínimo de la función en él, entonces el área del i-ésimo rectángulo elemental será mi(xi-xi-1) y el área total bajo la curva vendrá dada por
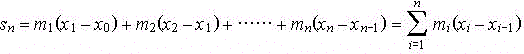
evidentemente será 
; con esto hemos acotado inferiormente el área buscada o, dicho
de otra forma, hemos calculado dicha área "por defecto".
Análogamente podríamos proceder para acotar superiormente el área sin más que ampliar cada uno de los rectángulos en que la hemos dividido hasta que sus alturas respectivas coincidan con los valores máximos de la función en cada intervalo. Sea, como antes, el intervalo [xi-1,xi] y Mi el máximo valor que alcanza la función en él, entonces el área del rectángulo así construido sobre este intervalo será Mi(xi-xi-1) y la suma de todos ellos
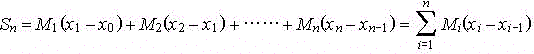
con lo que se tiene 
, es decir:
Por otra parte, habrás observado en las escenas anteriores que cuanto
mayor sea el número de subintervalos, las sumas anteriores se aproximan más y más al
área en cuestión. En particular si hacemos 
y f es continua, tendremos
Autor: José Mª Domínguez Torres