La función p(x)=a₀+a₁x+a₂x²+..........+a_nxⁿ, en la que los coeficientes a_k son constantes, se llama polinomio de grado n. En particular y=ax+b es un polinomio de primer grado e y=ax²+bx+c es un polinomio de segundo grado. Los polinomios pueden considerarse las funciones más sencillas de todas. Para calcular su valor para una x dada, necesitamos emplear únicamente las operaciones de adición, sustracción y multiplicación; ni siquiera la división es necesaria. Los polinomios son funciones continuas para todo x y tienen derivadas de cualquier orden. Además la derivada de un polinomio es también un polinomio de grado inferior en una unidad, y las derivadas de orden n+1 y superiores de un polinomio de grado n son nulas.

Si a los polinomios añadimos las funciones de la forma y=p(x)/q(x) (cociente de polinomios, para cuyo cálculo necesitamos también de la división), las funciones raíz cuadrada de x y raíz cúbica de x, y finalmente, las combinaciones aritméticas de los tipos anteriores, obtenemos esencialmente las funciones cuyos valores pueden calcularse por métodos aprendidos en el bachillerato.

A este nivel se tienen nociones de algunas otras funciones tales como log(x), sen(x), e^x, ..., pero, aunque se estudian sus propiedades más importantes, no se da una respuesta a las preguntas: ¿Cómo calcularlas? ¿Qué clase de operaciones, por ejemplo, es necesario realizar sobre la x para obtener log(x) o sen(x)?. La respuesta a estas preguntas la proporcionan los métodos desarrollados por el análisis matemático. Examinemos uno de estos métodos.

Fórmula de Taylor

Sea f(x) una función definida en un intervalo que contiene al punto a, con derivada de todos los órdenes.

El polinomio de primer grado p₁(x) = f(a) + f ' (a) (x-a) tiene el mismo valor que f(x) en el punto x=a y también, como se comprueba fácilmente, la misma derivada que f(x) en este punto. Su gráfica es una recta tangente a la gráfica de f(x) en el punto a.

Es posible elegir un polinomio de segundo grado, p₂(x) = f(a) + f ' (a) (x-a) + ½ f ' ' (a) (x-a)², tal que en el punto x=a tenga el mismo valor que f(x) y valores también iguales para su primera y segunda derivadas. Su gráfica en el punto a se acercará a la de f(x) más que la anterior. Es natural esperar que si construimos un polinomio que en x=a tenga las mismas n primeras derivadas que f(x) en el mismo punto, este polinomio se aproximará más a f(x) en los puntos x próximos a a. Así obtenemos la siguiente igualdad aproximada, que es la fórmula de Taylor:

f(x) ≈ f(a) + f '(a) (x-a) + (1/2!) f ' '(a) (x-a)² + ...... + (1/n!) f ⁽ⁿ⁾(a) (x-a) ⁿ

El segundo miembro de esta fórmula es un polinomio de grado n en (x-a). Para cada valor de x puede calcularse el valor de este polinomio se se conocen los valores de f(a) y de sus n primeras derivadas.

Para funciones que tienen derivada (n+1)-ésima, el segundo miembro de esta fórmula, como se demuestra fácilmente, difiere del primero en una pequeña cantidad que tiende a cero más rápidamente que (x-a)ⁿ. Además , es el único polinomio de grado n que difiere de f(x), para x próximo a a, en un valor que tiende a cero (cuando x tiende a a) más rápidamente que (x-a)ⁿ.
Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.

Para que sea exacta la igualdad aproximada anterior, debemos añadir al segundo miembro un término más, llamado resto:

f(x) = f(a)+f '(a)(x-a)+(1/2!) f ' '(a)(x-a)²+ ...... +(1/n!) f ⁽ⁿ⁾(a)(x-a)ⁿ+(1/(n+1)!) f ⁽ⁿ⁺¹⁾(c)(x-a)ⁿ⁺¹

El resto tiene la peculiaridad de que la derivada que en él aparece debe calcularse en cada caso, no en el punto a, sino en un punto c convenientemente elegido, desconocido, pero interior al intervalo de extremos a y x.

La demostración de la igualdad anterior es bastante engorrosa, aunque sencilla en esencia.

Las leyes naturales pueden expresarse, por regla general, con buena aproximación por funciones derivables un número arbitrario de veces, y por ello pueden ser aproximadas por polinomios cuyo grado viene determinado por la precisión deseada.

La fórmula de Taylor, que abre el camino para la mayoría de los cálculos en el análisis aplicado, es muy importante desde el punto de vista prático.

La idea de aproximar una función mediante polinomios o de representarla como suma de un número finito de funciones más sencillas alcanzó un gran desarrollo en el análisis, donde constituye ahora una rama independiente: la teoría de la aproximación de funciones.

En las siguientes escenas podemos observar cómo la gráfica de las funciones se va "tapando" con la gráfica del polinomio de Taylor al aumentar el grado del polinomio. Para un valor de x calculamos la diferencia entre el valor real y el valor del polinomio correspondiente. Al aumentar el grado del polinomio esa diferencia es cada vez menor. Hemos calculado los polinomios de Taylor para a=0.

1.- Aproximación de la función y = sen (x)

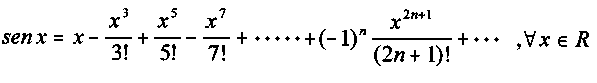
Actividades

1.- Observa que la función y=sen(x) es una función impar sen(-x)=-sen(x). El polinomio de Taylor correspondiente sólo tiene potencias impares de x.

2.- Da valores a x y observa como el polinomio de Taylor se aproxima al valor real al aumentar el grado del polinomio.

2.-Aproximación de la función y = cos (x)

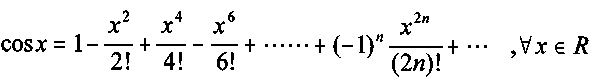
Actividades

1.- Observa que la función y=cos(x) es una función par cos(-x)=cos(x). El polinomio de Taylor correspondiente sólo tiene potencias pares de x.

2.- Da valores a x y observa como el polinomio de Taylor se aproxima al valor real al aumentar el grado del polinomio.

3.-Aproximación de la función y = e^x

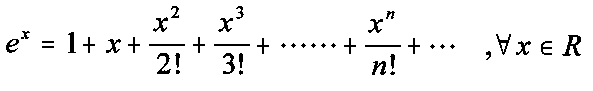
Actividades

1.- Observa que para x=1 obtenemos el valor del número e.

2.- Da valores a x y observa como el polinomio de Taylor se aproxima al valor real al aumentar el grado del polinomio.

4.-Aproximación de la función y = ln (1+x)

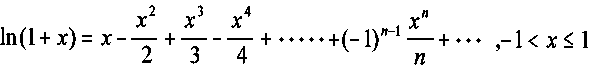
Actividades

1.- Da valores a x (entre -1 y 1) y observa como el polinomio de Taylor se aproxima al valor real al aumentar el grado del polinomio.

Autor:Mariano Banzo Marraco.