
DERIVADA DE UNA FUNCION
Definición e interpretación geométrica
1º.- Definición de derivada
La derivada es uno de los conceptos más importante en matemáticas. La derivada es el resultado de un límite y representa la pendiente de la recta tangente a la gráfica de la función en un punto. Pero vayamos por partes.
La definición de derivada es la siguiente:
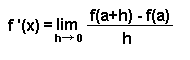
Podría, pues, no existir tal limite y ser la función no derivable en ese punto. En esta primera práctica vamos a ver que significa cada uno de los términos que aparecen en la formula anterior.
| Propuesta de
trabajo. 1º.- Comprueba en primer lugar como varía la llamada TVM (Tasa de variación media) de la funcion en un punto. Para ello varia el incremento
2º.- Comprueba los valores de las pendiente de las recta secantes y como varian al acercarse a la pendiente de la recta tangente. 3º.- Mueve el punto a lo largo de la curva. 4º.- Intenta encontrar un punto de la curva de tangente horizontal (es decir de pendiente 0) y un punto con recta tangente cuya pendiente sea 1 (Para ello , si es necesario, aumenta la escala) 5º.- Comprueba que al variar el punto, pero dejando fija la pendiente, varia la TVM dependiendo del punto |
2º.- Derivada de la parabola
Repetimos el ejrcicio anterior con una parabola
| Propuesta de
trabajo. 1º.- Comprueba en primer lugar como varía la llamada TVM (Tasa de variación media) de la funcion en un punto. Para ello varia el incremento
2º.- Comprueba los valores de las pendiente de las recta secantes y como varian al acercarse a la pendiente de la recta tangente. 3º.- Mueve el punto a lo largo de la curva. 4º.- Intenta encontrar un punto de la curva de tangente horizontal (es decir de pendiente 0) y un punto con recta tangente cuya pendiente sea 1 (Para ello , si es necesario, aumenta la escala) 5º.- Comprueba que al variar el punto, pero dejando fija la pendiente, varia la TVM dependiendo del punto |
3º.- Derivada de la parabola
Vemos otro ejemplo, con la misma función que el anterior. La escena muestra la recta tangente a la curva en cada punto y vamos comprobando que la pendiente de la recta tangente es la tangente trigonométrica del ángulo que forma la recta con el eje X
| Propuesta de
trabajo. 1º.- Varía el punto, abcisa, y comprueba como varia la recta tangente. 2º.- Observa como varía la tangente trigonometrica del ángulo que forman la recta tangente y el eje X 3º.- Mueve el punto a lo largo de la curva. 4º.- Intenta encontrar un punto de la curva de tangente horizontal (es decir de pendiente 0) y un punto con recta tangente cuya pendiente sea 1 (Para ello , si es necesario, aumenta la escala) 5º.- |
4º.- Función derivada de la cúbica.
Vamos a construir la función derivada. Esta función es una función que encada punto vale la pendiente de la recta tangene, es decir, la derivada de la función en cada punto.
| Propuesta de
trabajo. 1º.- Observa el dibuko de la gráfica de la derivada de la función cúbica en cada punto. 2º.- Comprueba que los valores de las pendiente de las recta tangente.son los valores de la función 3º.- Mueve el punto a lo largo de la curva para ir obteniendo la función derivada 4º.- Observa que los puntos de corte de la derivada son los puntos en donde la tangente es horizontal (posiblemente maximos y minimos) Intenta encontrar los maximos y los minimos de la cubica. Intenta encontrar un punto con recta tangente cuya pendiente sea 1 (Para ello , si es necesario, aumenta la escala) 5º.- Intenta encontrar un punto con recta tangente cuya pendiente sea 1 (Para ello , si es necesario, aumenta la escala) |
5º.- Función primera derivada y segunda derivada.
Vamos a construir la función derivada de una función polinómica de grado 4. Esta función será una función de grado 3. Ademas vamos a dibujar simultáneamente la función dervada segunda.
| Propuesta de
trabajo. 1º.- Observa el dibujo de la gráfica de la derivada y segunda derivada de la función cúbica. 2º.- Comprueba que los valores de las pendiente de las recta tangente.son los valores de la función 3º.- Mueve el punto a lo largo de la curva para ir obteniendo la función derivada y la segunda derivada. 4º.- Observa que los puntos de corte de la derivada son los puntos en donde la tangente es horizontal (posiblemente maximos y minimos). Observa que los puntos de corte de la segunda derivada son los puntos donde la función cambia de concava a convexa (puntos de INFLEXIÓN) |
Autor: Juan Avila