Resolución de triángulos rectángulos

Resolver un triángulo rectángulo es encontrar las medidas de sus tres lados y tres ángulos a partir de algunos de ellos que son conocidos. Para calcularlos hay que emplear algunas de las siguientes relaciones:

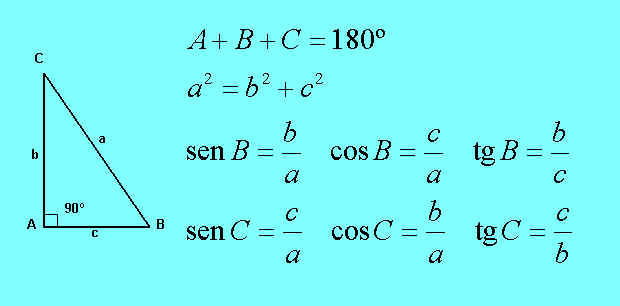
Analizaremos los dos casos posibles: Conocidos los dos lados, y conocidos un lado y un ángulo.

Conocidos los dos lados

El ejemplo típico es el de la escalera de una longitud conocida que se apoya en una pared y que se sitúa a una determinada distancia del suelo. Las incógnitas son el ángulo que forma la escalera con la pared y la altura que alcanza la escalera sobre ella. La escena permite simular este caso como si se tratara de apoyar la escalera en la pared e indica en cada momento el ángulo que forma con el suelo.

Mueve el punto C hasta que toque la línea vertical que representa la pared. Dibuja en tu cuaderno y calcula los valores del ángulo C y el lado b, teniendo en cuenta que cos C=c/a podrás hallar el ángulo y empleando el teorema de Pitágoras el lado b. Pulsa Inicio y repite el ejercicio para los valores a=8 y c=4.

Conocidos un lado y un ángulo

Supongamos que en un triángulo rectángulo se conoce el valor de uno de los catetos y el ángulo opuesto a él, por ejemplo, b y B. La escena ahora permite mover el vértice A hasta conseguir el ángulo C, complementario del B; en ese momento el triángulo queda resuelto.

Mueve el punto A y observa cómo varía el ángulo C; en el momento en que alcanza el valor complementario de B el triángulo queda resuelto. Resuelve el triángulo: b=4 y B=60º. Utiliza el seno para hallar el valor de la hipotenusa y después el teorema de Pitágoras para hallar el otro cateto. Pulsa Inicio y repite el ejercicio para b=8 y B=30

Autor: Miguel García Reyes

	Ministerio de Educación, Cultura y Deporte. Año 2000