| Fracciones Decimales Porcentajes |
11.- Cálculos con porcentajes |
| CÁLCULO DE UN TANTO POR CIENTO DE UNA CANTIDAD.- Para hallar un tanto por ciento de una cantidad, expresamos el tanto por ciento en forma decimal y multipliamos por él | |
| OBTENCIÓN DEL TANTO POR CIENTO CORRESPONDIENTE A
UNA PROPORCIÓN.- Para hallar qué tanto por ciento representa una cierta cantidad, a,
respecto a un total C, efectuamos |
Ejercicio 11
Calcula el :
a) 40% de 580.000 ptas.
b) 80% de 500
c) 5% de 250
d) 10% de 2980
e) 20% de 5 millones
f) 25% de 1
millón f) 30% de 3000
Todo lo puedes ver en la escena anterior.
Ejercicio 12
Calcula el tanto por ciento que representa:
a) 6320 de 15800 b) 96 de 480
c) 16 de 320
d) 750 de 5000
Comprueba en la escena anterior
| COMO SE CALCULAN AUMENTOS PORCENTUALES | |
| Un libro de 3.000 ptas. aumenta su
precio un 12% ¿Cuánto vale ahora? Aumento: 3000*0,12=360 ptas. Precio final: 3000+360=3360 ptas. Pero también podríamos haber hecho directamente: 3000*(1+0,12)=3000*1,12=3360 ptas. índice de variación-->1+0,12=1,12 |
|
| COMO SE CALCULAN DISMINUCIONES PORCENTUALES Un traje valía 42.000 ptas. y se rebaja un 25% ¿Cuánto vale ahora? Disminución: 42000*0,25=10500 ptas. Precio final: 42000-10500=31500 ptas. |
|
| Pero también
podríamos haber hecho directamente: 42000*(1-0,25)=42000*0,75=31500 ptas. índice de variación-->1-0,25=0,75 |
|
Ejercicio 13
Estos son algunos problemas que puedes resolver y comprobar con
la escena anterior:
a) El número de parados, 184.300, que había en una comunidad autónoma ha disminuido el
19% ¿Cuántos parados hay ahora?
b) En un pantano había 340 hl de agua. Ha disminuido un 43% ¿Cuánta agua queda en el
pantano?
c) Este año la gasolina ha subido un 5%. Si a principios de años costaba 135ptas/litro,
¿cuánto cuesta ahora el litro?
CÓMO SE ENCADENAN AUMENTOS Y DISMINUCIONES
PORCENTUALES
El coste de la vida subió un 10% en 1990 y un 8% en 1991. Pero en 1992 bajó un 5%
(estos datos no son reales). ¿Cuál fue la subida desde comienzos de 1990 hasta finales
de 1992?
Veamos en qué se transforma el precio de algo que valía 100
ptas. en enero de 1990:
(Puedes hacer los cálculos en la escena anterior)
| 100®(+10%)®100*1,10=110 | ||
| ¯ | ||
| 110®(+8%)®110*1,08=118,8 | ||
| ¯ | ||
| 118,8®(-5%)®118,8*0,95=112,86 | ||
Por tanto el aumento ha sido del 12,86% (Y no del 10+8-5=13%)
Ejercicio 14
La masa forestal de un bosque sufrió las siguientes variaciones
a lo largo de tres décadas:
de 1950 a 1960 aumentó un 28%
de 1960 a 1970 disminuyó un 40%
de 1970 a 1980 aumentó un 15%
¿Qué variación porcentual experimentó de 1950 a 1980?
Ejercicio 15
En un año el precio de un artículo sube un 40%, después baja un 10% y, por último, baja un 20% ¿Qué variación porcentual ha experimentado a lo largo del año?
CÓMO SE CALCULA LA CANTIDAD INICIAL
CONOCIENDO LA VARIACIÓN PORCENTUAL Y LA CANTIDAD FINAL
Después de haber aumentado su valor un 40%, el precio de una nevera es de 56000 ptas.
¿Cuál era su precio antes de la subida?
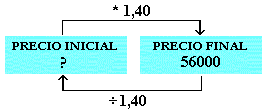
PRECIO INICIAL = 56000:1,40=40000 PTA.
Lo podemos ver en esta escena.
| Ejercicio 16 En las rebajas hemos comprado un cuadro por 17500 pta., una bicicleta por 8400 pta y un libro por 2730 pta. ¿Cuánto nos habría costado antes de las rebajas si todos los artículos tienen disminuido su precio en un 30%? Ejercicio 17 En unos grandes almacenes anuncian un 14% de descuento en todos sus artículos. Éstos son los precios que aparecen: |
| Pantalón de | 80 a | 70,4 euros | ¿Es cierto que han rebajado el 14%? Compruébalo |
| Camisa de | 35 a | 30 euros | |
| Jersey de | 54 a | 47,5 euros | |
| Camiseta de | 12 a | 10 euros | |
| Vaqueros de | 96 a | 85 euros |
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||