|
|
Fracciones Decimales Porcentajes |
|
|
Fracciones Decimales Porcentajes |
1.- Fracciones, decimales y porcentajes |
Cuando decimos "me he comido la
mitad del bocadillo", estamos usando una fracción: 
He dividido el bocadillo en dos partes iguales, 2
(denominador), y me he comido una de ellas, 1 (numerador)
En esta escena tenemos UNA UNIDAD, el
rectángulo rojo. Si quieres ver cuánto es , no tienes más que
dar en el botón inferior para que sea el denominador d=2,
después arrastras suavemente el punto A con el ratón, hasta
completar el primer rectángulo y el numerador sea n=1.
| Verás que aparece abajo la fracción La parte del rectángulo que se ha sombreado es El resto hasta completar LA UNIDAD será otro Si hacemos la división de 1 entre 2, nos sale 0.5, lo ves también en la escena. Así tenemos la fracción en forma de número
decimal.Pero hay más, esta fracción supone un 50% de la unidad. Basta multiplicar por 100 el decimal que nos ha salido, y tendremos el porcentaje. |
Con esta escena puedes ver muchas fracciones, pasarlas a forma
decimal y saber que % suponen de la unidad. Siempre serán de la forma 
Se obtienen dividiendo la unidad en tantas partes como diga el denominador d
(con el botón inferior), y tomando tantas partes como diga el numerador n
(moviendo el punto A)
En este caso sólo vamos a tomar en el numerador un número de partes inferior o igual al
denominador, debido a que sólo hemos representado una unidad. Mas adelante veremos los
demás casos.
Ejercicio 1
Representa en la escena anterior las siguientes fracciones,
pulsando el botón inicio, cada vez que quieras cambiar de fracción: 
, y anota qué
fracción representa la zona que no está sombreada hasta completar LA UNIDAD.
Efectúa las divisiones con la calculadora y comprueba las
expresiones decimales y en porcentaje de cada una de ellas.
Para esta escena puedes coger otras fracciones que quieras, pero siempre con el numerador
menor o igual que el denominador.
Ejercicio 2
| 1) Representa en esta escena una fracción, por
ejemplo 1/3 (ya sabes denominador=3 en el botón de abajo, y numerador =1 arrastrando el punto A) 2) Pulsa el botón del denominador una vez (d=4), y verás que la UNIDAD ha quedado dividida en cuatro partes iguales (cada una será 1/4), pero que la zona sombreada no coincide con ninguna de ellas, y que la fracción tiene un número decimal en el numerador. NO NOS VALE. 3) Pulsa de nuevo el botón denominador (d=5), la UNIDAD ha quedado dividida en cinco partes (cada una será 1/5) y vuelve a ocurrir lo mismo. |
|
| 4) Pulsa de nuevo el botón denominador
(d=6) ahora la UNIDAD ha quedado dividida en seis partes (cada una será 1/6), pero la zona sombreada coincide exactamente con dos de esas partes. Ahora la fracción es 2/6, y es exactamente la misma cantidad que el 1/3 que teníamos al principio. Eso quiere decir que 1/3=2/6, son dos FRACCIONES EQUIVALENTES. |
|
| 5) Puedes seguir pulsando el botón denominador, hasta que vuelva a coincidir la zona sombreada inicialmente con las partes en que va quedando dividida la UNIDAD. Ve anotando las sucesivas fracciones equivalentes. ¿Qué operaciones se ha hecho en cada fracción para obtener la siguiente equivalente? | |
Dada una fracción 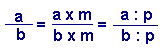 , para obtener una fracción equivalente,
basta multiplicar o dividir, numerador y denominador por un mismo número. Así:  |
y
represéntalas en la escena anterior para comprobar que representan el mismo número.Pero cuando no las podemos
representar, ¿cómo averiguamos si dos fracciones son equivalentes?
pues muy fácil. Por ejemplo si quiero saber si 
, basta comprobar que 12x10=15x8=120
¿Son equivalentes las fracciones 
? ¿y 
y ?
Compruébalo en la escena anterior.
Otra forma de comprobar si dos fracciones son equivalentes es efectuando la división del
numerador entre el denominador.
|
Se trata de obtener fracciones equivalentes, pero
con el mismo denominador.
Vamos a reducir a común denominador las fracciones 
a) Mínimo común múltiplo (m.c.m.) de 4 y 6 = 12. Éste va a ser
el denominador común, que dividimos por cada denominador.
b) 12:4 = 3; Hay que multiplicar por 3; 
c) 12:6=2; Hay que multiplicar por 2;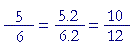 
Ahora tenemos dos fracciones equivalentes a las primeras, pero con el mismo denominador.
Introduce el valor del m.c.m. de los denominadores en esta escena, y pulsa el botón
solución de 0 a 1, podrás ver las fracciones reducidas a común denominador.
Ejercicio 4
Reduce a común denominador las fracciones:
a) 5/4 y 7/18 b)
7/3 y 8/27 c) 4/7 y 5/14
d) 3/100 y 5/4
Comprueba tus resultados en la escena anterior.
Puedes introducir las fracciones que quieras y reducirlas a común denominador.
Introduce en esta escena las fracciones 3/9 y 7/9, que tienen el mismo denominador (los denominadores en los botones inferiores, los numeradores arrastrando con el ratón los puntos A y B). ¿Cuál es mayor?
Ahora introduce las fracciones 3/4 y 3/7, que tienen el mismo numerador. ¿Cuál es mayor?
| De dos fracciones con el mismo denominador es mayor la de numerador mayor |
| De dos fracciones con el mismo numerador es mayor la de denominador menor |
Si quieres comparar dos fracciones que no tienen igual ni numerador ni denominador, redúcelas a común denominador y luego las comparas, o bien haces la división de numerador entre denominador y comparas los cocientes resultantes.
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||
