
Condición para que cuatro puntos sean concíclicos
Vamos a estudiar una propiedad interesante que cumplen cuatro puntos que están en una circunferencia (puntos concíclicos).
La imagen ![]() aparecerá algunas veces al final de un párrafo, es un enlace a una
página de ayuda. Utilízala sólo después de
haber reflexionado sobre la cuestión propuesta.
aparecerá algunas veces al final de un párrafo, es un enlace a una
página de ayuda. Utilízala sólo después de
haber reflexionado sobre la cuestión propuesta.
PIENSA:
Si los cuatro puntos
fueran vértices de un rectángulo ¿Pertenecen a la misma circunferencia?.
¿Cómo se obtendría el centro? ¿Qúe longitud tiene el radio?![]()
Si los cuatro puntos
fueran vértices de un paralelogramo, no rectángulo, ¿Pueden pertenecer a
una circunferencia?![]()
Si te dan cuatro
puntos cualesquiera en el plano, ¿Cómo harías, con los conocimientos
previos, para
saber si están en una misma circunferencia? ![]()
EXPERIMENTA CON EL NIPPE DESCARTES:
Observa el NIPPE DESCARTES
Se consideran cuatro puntos en el plano A, B, C y D.
A y B determinan una recta r
C y D determinan otra recta s
Suponemos que r y s no son paralelas (rectas secantes)...se cortan en un punto P.
Inicialmente hemos situado A y C a la misma distancia de P. Lo mismo ocurre con B y D.
El punto Q es el corte de las mediatrices de los segmentos AB y CD
En este caso comprobarás que están sobre una circunferencia de centro Q y radio r = QA = QB = QC = QD. Para ver la circunferencia introduce el parámetro r correspondiente (r = 2.74) y pulsa limpiar.
4.
¿Por
qué, en este caso, los cuatro puntos equidistan de Q (centro de la
circunferencia? ![]()
En este caso resulta evidente que PAxPB = PCxPD
Cambia la posición del punto A, por ejemplo, y advierte que QA = QB <> QC = QD, por lo que los los cuatro puntos no estan en la circunferencia de centro Q, a la vez que PAxPB <> PCxPD
Para modificar la posición de los puntos se puede pinchar y arrastrar con el ratón sobre el punto ó cambiar en la ventana de parámetros del NIPPE los desplazamientos horizontales ax, bx, cx, dx de dichos puntos respecto de la posición del punto P.
Se nos puede ocurrir la siguiente idea: Si cambiamos de posición A, B, C y D pero de tal manera que se cumpla PAxPB = PCxPD, ¿los puntos pertenecerán a la circunferencia de centro Q?
Intentemos convencernos de que esto es así. Cambiemos de posición los puntos A, B, C y D tratemos de hacer ajustes con las distancias PA, PB, PC y PC hasta que se cumpla PAxPB = PCxPD
Empecemos por reiniciar el NIPPE para que el radio tome el valor 0 y la circunferencia se oculte.
Posicionemos A en ax=4.00, B en bx=5.50. Observa como los cuatro puntos no están todos equidistantes de Q (intersección de las mediatrices de los segmentos AB y CB) donde debe estar el centro de la circunferencia.
Posicionesmos C en cx=2.50 y D en dx=8.80
Ahora, nuevamente, se cumple la igualdad "mágica" PAxPB=PCxPD=24.44
Este producto no es el mismo que en el ejemplo inicial, pues las distancias PA, PB, PC y PD han cambiado.
Las distancias de los cuatro puntos al punto Q son todas iguales QA=QB=QC=QD=3.34
Visualiza la circunferencia para comprobar el resultado entrando el valor r = 3.34 en la ventana de parámetros y pulsando limpiar.
DEFINICIÓN: POTENCIA DE UN PUNTO RESPECTO DE UNA CIRCUNFERENCIA
|
Si desde un punto P trazamos una secante a una circunferencia, el producto de las distancias de los puntos de corte sobre la circunferencia al punto P es constante (PAxPB=constante). A este producto se le llama POTENCIA del punto P respecto de la circunferencia. |
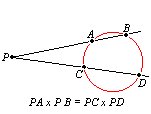 |
Observaciones:
El punto P puede ser exterior, interior o pertenecer a la circunferencia.
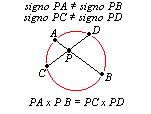
Si el punto es interior las distancias PA y PB son de signos opuestos (pues para ir de P a A se hace en sentido contrario sobre la recta al que se hace para ir de P a B. Por tanto si el P punto es es exterior a la recta, tiene potencia positiva y si es interior tiene potencia negativa.
Un punto P que esté sobre la circunferencia tendrá potencia 0. ¿Por qué?
EJERCICIOS:
Actuando sobre el Nippe DESCARTES, dibuja la circunferencia tal que la potencia del punto P respecto de ella valga 11.35
Posiciona cuatro puntos concíclicos.
Dibuja una cicunferencia interior al punto P tal que su potencia sea -7.66
¿Dónde debes posicionar los puntos A y B para que la pontencia de P sea 0? ¿Qué pasa ahora con los puntos C y D?
EXPERIMENTA CON LA SIGUIENTE ESCENA
Observaciones: Se pueden modificar desde la ventana de parámetros, los siguientes:
Radio r de la circunferencia respecto de la que se calcula la potencia del punto P
Coordenada del centro C(Cx,Cy)
lugC, es el radio de valor PC de la circunferencia de centro P. Introduce el valor 5.09 en la ventana del parámetro lugC y pulsa limpiar, verás el lugar de centros C con radio 5.09 (valor actual de PC). Después de visto pulsa inicio.
lugP, es el radio de valor PC de la circunferencia de centro C. Introduce el valor 5.09 en la ventana del parámetro lugP y pulsa limpiar, verás el lugar de puntos P con radio 5.09 (lugar actual de PC). Después de visto pulsa inicio.
lugT, es el radio de valor PT de la circunferencia de centro P. Introduce el valor 4.69 en la ventana del parámetro lugT y pulsa limpiar, verás el lugar de puntos T con radio 4.69 (lugar actual de PT). Después de visto pulsa inicio.
Estas observaciones ter permitirán contestar algunas preguntas.
Reflexiona sobre las siguientes cuestiones, experimenta en la anterior escena DESCARTES y trata de dar respuesta.
Si trazamos una
recta desde P que pase por el centro C
de la circunferencia ¿Cuáles son
los puntos de corte? ¿Cómo podemos expresar, en este caso la
potencia de P respecto de la circunferencia?
![]()
Si la recta
trazada desde P es tangente a la circunferencia entonces hay un solo punto T
de corte (punto de tangencia). ¿ Se cumple que PT
x PT = PT2
es la potencia de P respecto de la circunferencia?
![]()
Dado un punto P
exterior a una circunferencia, su potencia podrá ser 22, como en el
ejemplo inicial siguiente.
¿Existirán otras circunferencias con el mismo radio r respecto de las cuales P
tenga la misma potencia 22?
![]()
¿Cual es el lugar
de centros
de todas las circunferencias de igual radio que tiene la misma potencia para
P? ![]()
¿Habrá
circunferencias con distinto radio y con la misma potencia de P respecto de
ellas? ![]()
¿A qué distancia
de P se encuentran los centros de todas las circunferencias de radio 2 con
potencia 30 ? ![]()
Llamamos d
a la distancia del punto P
al centro de la circunferencia (PC = d), siendo r
el radio. Demuestra que si el punto P
es exterior la potencia se puede
expresar por d2-r2 .
![]()
¿Existen
distintos puntos que tengan la misma potencia respecto de la circunferencia
de radio r y centro C? ![]()
SOLUCIONES:
1. Traza las diagonales. Estas se cortan en el punto medio. Como las diagonales son iguales, el punto medio de ambas es común y equidistan de los cuatros vértices. Por tanto éstos son concíclicos.
2. No. Si trazamos las mediatrices dos lados paralelos (opuestos) estás no se cortan, por tanto no existe centro de la circunferencia que contenga a los cuatro puntos.
3. Trazamos el cuadrilátero y una diagonal. Quedará dividido en dos triángulos. Si los cuatro vértices son concíclicos, las tres mediatrices trazadas dobre la diagonal y dos lados opuestos tienen que cortarse en centro de la circunferencia.
4. Se cumple que PA=PC y PB=PD, por lo que AB=CD y el punto Q pertenece a la bisectriz del ángulo con vértice en P. Los segmentos AB y CD son simétricos respecrto de la recta PQ y las distancias AQ y CQ son iguales (lo mismo ocurre con las distancias BQ y DQ).
Como Q es de la mediadriz de AB se cumple que AQ = BQ.
Como Q es de la mediatriz de CD se cumple que CQ = DQ.
Consecuentemente AQ = BQ =CQ =DQ y los cuatro puntos pertenecen a la circunferencia de centro Q.
5. Los puntos de corte son E y F diametralmente opuestos. La potencia será PExPF.
6. Efectivamente se puede comprobar que la potencia de P respecto de la circunferencia de centro C y radio r es el cuadrado de la distancia PT. Pues si regresas al concepto de potencia, en el dibujo abjunto, la potencia es PAxPB donde A y B son los puntos de corte con la circunferencia de la recta secante trazada desde P. La tangente a la circunferencia trazada desde P se puede considerar como un caso límite en el que los dos puntos de corte A y B coinciden PA=PB=PT, luego PAxPB=PT2 .
7. Dibuja la circunferencia de centro P y radio PC (introduce lugC=PC y pulsa limpiar). Comprueba que las circunferencias de radio r que tengan su centro sobre aquella cumplen la condición.
8. Dibuja la circunferencia de radio PC y centro P (introducir lugC=PC y pulsa limpiar), si mueves el centro de C sobre dicha circunferencia comprobarás que la potencia respecto de P es la misma que antes.
9. Dibuja la circunferencia de radio PT y centro P ( introducir lugT=PT y pulsar limpiar), cambia el radio r (introducir, por ejemplo r=3), cambia la posición del centro C hasta conseguir que la distancia PT valga lo mismo que valía antes (lugT).
10. Cambia las posición del centro C, modificando sus coordenadas, hasta conseguir que la potencia valga 30 y lee el valor de la distancia PC.
11. Efectivamente, siendo PE=d+r y PF = d-r, se cumple que la potencia de P respecto de la circunferencia es PExPF=(d+r)(d-r).
12. Dibuja la circunferencia de centro C y radio PC (introduce lugP=PC y pulsa limpiar). Es evidente que cualquier punto de este lugar dista del centro C lo mismo PC=d, así pues tendrán la misma potencia respecto de la circunferencia de centro C y radio r; es decir el mismo valor de la expresión (d+r)(d-r)
Autor: Ángel Cabezudo Bueno
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||