
Un lugar geométrico es un conjunto de puntos que satisfacen una misma propiedad. Por ejemplo: la circunferencia, la elipse, la mediatriz de un segmento, la bisectriz de un ángulo, etc.
Un lugar geométrico interesante:
ARCO CAPAZ
| En la figura vemos a unos futbolistas en posición de lanzar el balón contra la portería. El ángulo de tiro es el formado por el pié del jugador (vértice) y las trayectorias a los postes (lados). ¿Qué posiciones deberán ocupar los jugadores para que todos tengan el mismo ángulo de tiro? | 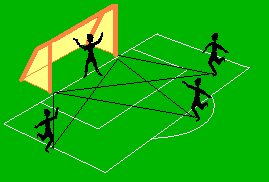 |
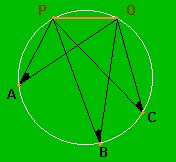 |
El problema consiste en averiguar el lugar
geométrico de los puntos del plano desde los cuales se ve el ancho de
la portería con el mismo ángulo.
Este problema está relacionado con la propiedad de los ángulos inscritos en una circunferencia que abarcan el mismo arco PQ (misma cuerda). Sabemos que estos ángulos miden todos lo mismo: la mitad del ángulo central correspondiente. |
RESOLUCIÓN DEL PROBLEMA:
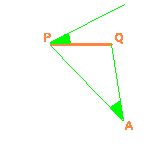
Supongamos que el ángulo de tiro es de 35º y que la portería se interpreta como un segmento PQ. Vamos a construir el arco de circunferencia. Debemos saber que tanto los ángulos inscritos como el ángulo semiinscrito que abarcan la misma cuerda PQ miden lo mismo. En la figura adjunta el ángulo semiinscrito es el que tiene el vértice en la circunferencia, punto P, un lado es tangente en P y el otro lado es secante en Q |
 |
Observemos la siguiente escena del NIPPE DESCARTES:
|
EXPERIMENTEMOS CON EL NIPPE DESCARTES...
Observaciones:
El punto A, es un control que puedes deplazar pinchando y arrastrando con el puntero del ratón. Éste se desplaza por el arco capaz de cada una de las dos circunferencias simétricas. Comprobar como el ángulo con vértice en A no cambia de valor a lo largo del recorrido.
Si cambiamos los parámetros ángulo ó cuerda PQ el lugar geométrico cambia también, por lo que para ver la escena adaptada a la nueva situación tendremos que pulsar limpiar y llevar el punto control A al nuevo arco.
El texto de la escena te permite conocer:
El Centro C de la circunferencia, referido al origen (0,0) situado en el centro de la cuerda PQ. El centro C' de la otra circunferencia es simétrico respercto de PQ.
El radio de las circunferencias PC = PC´
La longitud de cada uno de los arcos capaces.
Tener en cuenta esta información para resolver los problemas siguientes.
PROBLEMAS:
Determinar el arco capaz desde el cual se ve el segmento PQ = 6 con bajo un ángulo de 50,5 º.
Dibuja en tu cuaderno, la solución del problema anterior y comprueba el resultado consultando la posición del centro y el radio de la circunferencia.
Calcula
la longitud del arco capaz del problema anterior y comprueba el resultado
obtenido por el NIPPE![]()
Si mantenemos constante el segmento PQ, y aumentamos el ángulo ¿El radio de la circunferencia, aumenta o disminuye? Reflexiona antes de resolver.
Utilizando
la construcción del arco capaz, dibuja en tu cuaderno, un triángulo,
conocidos el lado BC = 6cm;
el ángulo opuesto, A = 45º
y la mediana ma = 5 cm ![]()
SOLUCIONES:
3. La medida del ángulo central que abarca el arco capaz es 360º - 2* 50.5º = 360º -101º = 259º. Pasando a radianes se tiene 259º * 3.1416/180º = 4.5204 y multiplicando por la medida del radio obtenemos 3.88*4.5204 = 17.54. La diferencia con el resultado del NIPPE, 17.57, se debe a que éste trabaja con más precisión, por ejemplo al tomar el número pi con más decimales.
5. Se dibuja el arco capaz desde el cual se ve el segmento BC bajo un ángulo de 45º. Con centro en el punto medio de BC se traza una circunferencia que tenga por radio la mediana ma = 5 cm. Las intersecciones de la circunferencia y el arco capaz son los vértices A posibles del triángulo, es decir el problema tiene dos soluciones.
Autor: Ángel Cabezudo Bueno
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||