Razones trigonométricas de ángulos agudos

Razones trigonométricas en un triángulo rectángulo

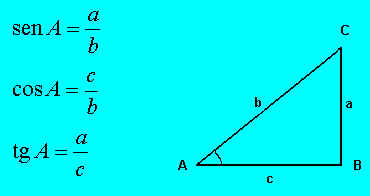
Las razones trigonométricas de un ángulo agudo se definen en función de los lados de ese triángulo y son independientes de su tamaño.Las razones trigonométricas  seno, coseno y tangente del ángulo agudo de un triángulo rectángulo como el de la figura, en el que el ángulo B=90º, b es la hipotenusa, y a y c son los catetos,  se definen así:

Si se aumenta el tamaño de los lados del triángulo ABC prolongando los lados b y c y trazando rectas paralelas al lado a se obtienen triángulos semejantes al anterior y, por tanto, las razones trigonométricas del ángulo A siguen siendo las mismas, dependiendo sólo de su amplitud (en grados o radianes). Empleando la escena del Nippe Descartes vamos a poder comprobar esta propiedad.

Varía los valores de b hasta que alcance una longitud de 12. Observa cómo no varía el valor de las razones trigonométricas del ángulo de 30º que aparece en la figura.  Cambia a 45º y 60º. Calcula las razones trigonométricas de los ángulos de 15º, 1 radián, 85º y 0.3 radianes. Intenta construir un triángulo rectángulo de lados 3, 4 y 5. ¿Qué valor toma el ángulo A?

Un triángulo de hipotenusa unidad

Puesto que el valor de las razones trigonométricas en un triángulo rectángulo no dependen del tamaño de los lados, puede elegirse un triángulo cuya hipotenusa sea b=1. En este caso los cálculos se simplifican considerablemente, de forma que el cateto opuesto al ángulo es igual al seno y el contiguo al coseno. Empleando este triángulo de hipotenusa unidad se puede encontrar el ángulo al que corresponde un determinado valor de una razón trigonométrica.

Repite en este caso el cálculo de las razones trigonométricas de los ángulos de 15º, 45º, 60º, 1 radián, 85º y 0.3 radianes. ¿Encuentras alguna relación entre las tres razones trigonométricas? Intenta escribir una fórmula que las relacione.

Calcula el valor del ángulo A en los casos en que: sen A=0.5, cos A=0.75 y tg A=2.75

Relación fundamental de la trigonometría

Teniendo en cuenta el triángulo de hipotenusa unidad, si aplicamos el teorema de Pitágoras, se debe cumplir que

Esta expresión se conoce como relación fundamental de la trigonometría y junto con la que relaciona a la tangente con el seno y el coseno de un ángulo permite calcular las restantes razones trigonométricas a partir de una de ellas.

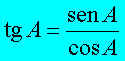
Comprueba para diferentes valores del ángulo A que se cumplen las relaciones anteriores entre sus razones trigonométricas. Si el seno de un ángulo es 1/3 calcula las restantes razones trigonométricas. Repite la operación si el coseno de un ángulo es . ¿Sabrías calcular el valor del seno y el coseno cuando la tangente del ángulol es 1?

Razones trigonométricas de ángulos complementarios

Como la suma de los ángulos de cualquier triángulo es 180º, en un triángulo rectángulo los dos ángulos agudos deben sumar 90º. Se dice también que dos ángulos que suman 90º son complementarios. El programa Descartes muestra ahora simultáneamente los valores de las razones trigonométricas de los ángulos A y C, que ya sabemos que son complementarios.

¿Encuentras alguna relación entre las razones trigonométricas? Prueba con A: 45º, 60º, 33.4º, 72º y 85,7º. ¿Se mantienen las relaciones anteriores entre las razones de A y C? Si se conocen el sen A=0.391 y cos A=0.921 ¿Sabrías calcular la tg A y las tres razones trigonométricas del ángulo complementario de A?

Autor: Miguel García Reyes

	Ministerio de Educación, Cultura y Deporte. Año 2000