
MEDIDAS EN UNA TRAMA
-
I. Segmentos en una trama 5x5
-
Dos puntos cualesquiera en la trama determinan un
segmento
cuya longitud puedes obtener fácilmente tomando como unidad de medida la
distancia que hay entre dos puntos consecutivos de la trama. Para ello considera
el segmento como hipotenusa de un triángulo rectángulo cuyos catetos son
fácilmente deducibles. Explora, moviendo los puntos mediante los cursores,
distintas segmentos.
En el ejemplo inicial, los catetos miden 3 y 2
unidades respectivamente y eso nos permite obtener para el
segmento una medida de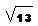 , aunque en el dibujo aparezca 3,61 como
aproximación.
, aunque en el dibujo aparezca 3,61 como
aproximación.
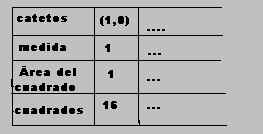
1) Para encontrar todas las medidas posibles de
los segmentos en la trama, deberás hacerlo de una manera
sistemática. Para ello te puedes ayudar de una tabla como la que
hay a continuación y que deberás rellenar en tu cuaderno.

2) Ayudándote de una tabla como la anterior,
escribe en tu cuaderno las medidas de todos los segmentos
posibles en una trama de 6x6 puntos.
II.Cuadrados en una trama 5x5.
Se trata de encontrar el mayor número
posible de cuadrados en
una trama 5x5, que tengan, claro está, sus vértices sobre ella.
A modo de ejemplo, si partes del segmento de vértices A y B,
puedes colocar los puntos C y D de manera que el polígono ABCD
sea un cuadrado. Lleva el segmento de extremos A y B a otro lugar
mediante sus coordenadas, manteniendo su medida, e intenta
encontrar un nuevo cuadrado moviendo directamente los puntos C y
D sobre la trama.
3) Encuentra el número total de cuadrados que puedes
construir sobre la trama 5x5, que tengan de lado cada una de las
medidas halladas en la actividad anterior.
Debes organizar bien la información para no dejarte ningún
cuadrado. Para ello, parte de la tabla anterior y completa dos
nuevas filas.
III.Triángulos rectángulos en una
trama 5x5.
Dados los puntos A y B, se trata de
situar un tercer punto P, sobre la trama, de modo que los tres
formen un triángulo
rectángulo. Encuentra todas las
soluciones posibles para P manteniendo fijos A y B. Considera dos
soluciones iguales si corresponden a triángulos superponibles.
Si tienes dudas, halla la medida de los lados como se ha indicado
en la actividad I y comprueba si verifican el Teorema de
Pitágoras.
4) Coloca los puntos A y B en distintas posiciones y,
para cada una de ellas, encuentra todas las soluciones para P.
5) ¿Hay pares de puntos A y B para los que no exista
un punto P que forme con ellos un triángulo rectángulo?
IV. Triángulos que tienen una base igual a la
altura correspondiente.
En el triángulo
de la figura podemos tomar el lado AB como base de medida 1. Su
altura también es 1, pero es posible obtener distintos
triángulos de altura 1 moviendo paralelamente a la base el punto
P. Puedes ver que hay 4 triángulos distintos con base y altura
1.
.
6) Haz que la base AB sea 2 y busca, moviendo el punto
P, los distintos triángulos de altura 2.
7) Completa todas las posibilidades para las distintas
medidas existentes hasta encontrar las 22 soluciones que hay. De
nuevo, deberás recoger todos los datos en una tabla en tu
cuaderno.
 |
|
|
Ministerio de Educación, Cultura y Deporte. Año 2000 |
|
| |


